题目内容
【题目】已知函数![]() 的图像过点
的图像过点![]() 和
和![]() .
.
(1)求函数![]() 的解析式;
的解析式;
(2)若![]() 在
在![]() 上有解,求
上有解,求![]() 的最小值;
的最小值;
(3)记![]() ,
,![]() ,是否存在正数
,是否存在正数![]() ,使得
,使得![]() 对一切
对一切![]() 均成立?若存在,求出
均成立?若存在,求出![]() 的最大值;若不存在,说明理由.
的最大值;若不存在,说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ,理由见解析
,理由见解析
【解析】
(1)直接把点![]() 和
和![]() 的坐标代入函数方程求出
的坐标代入函数方程求出![]() ,
,![]() 的值,即可求函数
的值,即可求函数![]() 的解析式;(2)原方程等同于
的解析式;(2)原方程等同于![]() 在
在![]() 上有解,结合单调性求出右端最小值即可;(3)先根据条件求出数列
上有解,结合单调性求出右端最小值即可;(3)先根据条件求出数列![]() 的通项公式,将题意转化为
的通项公式,将题意转化为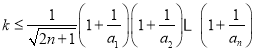 恒成立;再通过构造
恒成立;再通过构造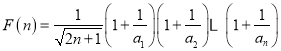 ,利用其单调性求出
,利用其单调性求出![]() 的最小值即可求出
的最小值即可求出![]() 的最大值.
的最大值.
(1)由已知得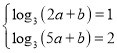 ,解得
,解得![]() ,
,
∴![]() .
.
(2)由(1)得![]() 在
在![]() 上有解,
上有解,
即![]() 在
在![]() 上有解,
上有解,
令![]() ,易得
,易得![]() 在
在![]() 上单调递增,
上单调递增,
![]() ,即
,即![]() 的最小值为2.
的最小值为2.
(3)因为![]() ,
,
假设存在正数![]() ,使得
,使得![]() 对一切
对一切![]() 均成立,
均成立,
则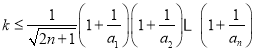 恒成立.
恒成立.
记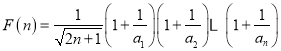 ,
,
则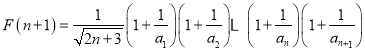 ,
,
∵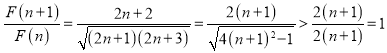 ,
,
∴![]() ,所以
,所以![]() 是递增数列.
是递增数列.
所以![]() 时
时![]() 最小,最小值
最小,最小值![]() ,
,
所以![]() ,即
,即![]() 的最大值为
的最大值为![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目