题目内容
【题目】某学校组织了垃圾分类知识竞赛活动.设置了四个箱子,分别写有“厨余垃圾”、“有害垃圾”、“可回收物”、“其它垃圾”;另有卡片若干张,每张卡片上写有一种垃圾的名称.每位参赛选手从所有卡片中随机抽取![]() 张,按照自己的判断,将每张卡片放入对应的箱子中.按规则,每正确投放一张卡片得
张,按照自己的判断,将每张卡片放入对应的箱子中.按规则,每正确投放一张卡片得![]() 分,投放错误得
分,投放错误得![]() 分.比如将写有“废电池”的卡片放入写有“有害垃圾”的箱子,得
分.比如将写有“废电池”的卡片放入写有“有害垃圾”的箱子,得![]() 分,放入其它箱子,得
分,放入其它箱子,得![]() 分.从所有参赛选手中随机抽取
分.从所有参赛选手中随机抽取![]() 人,将他们的得分按照
人,将他们的得分按照![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分组,绘成频率分布直方图如图:
分组,绘成频率分布直方图如图:
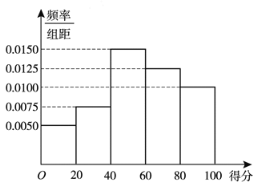
(1)分别求出所抽取的![]() 人中得分落在组
人中得分落在组![]() 和
和![]() 内的人数;
内的人数;
(2)从所抽取的![]() 人中得分落在组
人中得分落在组![]() 的选手中随机选取
的选手中随机选取![]() 名选手,以
名选手,以![]() 表示这
表示这![]() 名选手中得分不超过
名选手中得分不超过![]() 分的人数,求
分的人数,求![]() 的分布列和数学期望;
的分布列和数学期望;
(3) 如果某选手将抽到的20张卡片逐一随机放入四个箱子,能否认为该选手不会得到100分?请说明理由.
【答案】(1)抽取的![]() 人中得分落在组
人中得分落在组![]() 的人数有
的人数有![]() 人,得分落在组
人,得分落在组![]() 的人数有
的人数有![]() 人;(2)分布列见解析,1.2;(3)答案不唯一,具体见解析.
人;(2)分布列见解析,1.2;(3)答案不唯一,具体见解析.
【解析】
(1)根据频率分布直方图即可得到满足题意的人数;
(2)![]() 的所有可能取值为
的所有可能取值为![]() ,
,![]() ,
,![]() ,求出相应的概率值,即可得到的分布列和数学期望;
,求出相应的概率值,即可得到的分布列和数学期望;
(3)该选手获得100分的概率是![]() ,结合此数据作出合理的解释.
,结合此数据作出合理的解释.
(1)由题意知,所抽取的![]() 人中得分落在组
人中得分落在组![]() 的人数有
的人数有![]() (人),
(人),
得分落在组![]() 的人数有
的人数有![]() (人).
(人).
所以所抽取的![]() 人中得分落在组
人中得分落在组![]() 的人数有
的人数有![]() 人,得分落在组
人,得分落在组![]() 的人数有
的人数有![]() 人.
人.
(2)![]() 的所有可能取值为
的所有可能取值为![]() ,
,![]() ,
,![]() .
.
![]() ,
, ![]() ,
, ![]() .
.
所以![]() 的分布列为
的分布列为
|
|
|
|
|
|
|
|
所以![]() 的期望
的期望![]() .
.
(3)答案不唯一.
答案示例1:可以认为该选手不会得到100分.理由如下:
该选手获得100分的概率是![]() ,概率非常小,故可以认为该选手不会得到100分.
,概率非常小,故可以认为该选手不会得到100分.
答案示例2:不能认为该同学不可能得到100分.理由如下:
该选手获得100分的概率是![]() ,虽然概率非常小,但是也可能发生,故不能认为该选手不会得到100分.
,虽然概率非常小,但是也可能发生,故不能认为该选手不会得到100分.

【题目】某学校数学建模小组为了研究双层玻璃窗户中每层玻璃厚度![]() (每层玻璃的厚度相同)及两层玻璃间夹空气层厚度
(每层玻璃的厚度相同)及两层玻璃间夹空气层厚度![]() 对保温效果的影响,利用热传导定律得到热传导量
对保温效果的影响,利用热传导定律得到热传导量![]() 满足关系式:
满足关系式: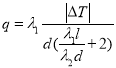 ,其中玻璃的热传导系数
,其中玻璃的热传导系数![]() 焦耳/(厘米
焦耳/(厘米![]() 度),不流通、干燥空气的热传导系数
度),不流通、干燥空气的热传导系数![]() 焦耳/(厘米
焦耳/(厘米![]() 度),
度), ![]() 为室内外温度差.
为室内外温度差.![]() 值越小,保温效果越好.现有4种型号的双层玻璃窗户,具体数据如下表:
值越小,保温效果越好.现有4种型号的双层玻璃窗户,具体数据如下表:
型号 | 每层玻璃厚度 (单位:厘米) | 玻璃间夹空气层厚度 (单位:厘米) |
A型 |
|
|
B型 |
|
|
C型 |
|
|
D型 |
|
|
则保温效果最好的双层玻璃的型号是________型.