题目内容
6.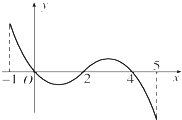 已知函数f(x)的定义域为[-1,5],f(x)的导函数f′(x)的图象如图所示.若f(x)在区间[m,m+1]上是单调函数,则实数m的取值范围是{m|m=-1或0≤m≤1或2≤m≤3或m=4}.
已知函数f(x)的定义域为[-1,5],f(x)的导函数f′(x)的图象如图所示.若f(x)在区间[m,m+1]上是单调函数,则实数m的取值范围是{m|m=-1或0≤m≤1或2≤m≤3或m=4}.
分析 先求出函数的单调区间,从而得到区间[m,m+1]所在的范围,求出即可.
解答 解:由图象得:函数f(x)在[-1,0)递增,在(0,2)递减,在(2,4)递增,在(4,5]递减,
∴[m,m+1]⊆[-1,0]或[m,m+1]⊆[0,2],或[m,m+1]⊆[2,4],或[m,m+1]⊆[4,5],
∴m=-1或0≤m≤1或2≤m≤3或m=4,
故答案为:{m|m=-1或0≤m≤1或2≤m≤3或m=4}.
点评 本题考查了函数的单调性问题,考查导数的应用,数形结合思想,是一道基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.已知条件p:x>1,q:$\frac{1}{x}$<1,则¬p是¬q成立的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
14.针对时下的网购热,某单位对“喜欢网购与职工性别是否有关”进行了一次调查,其中男职工有60人,女职工人数是男职工人数的$\frac{1}{2}$,喜欢网购的男职工人数是男职工人数的$\frac{1}{6}$,喜欢网购的女职工人数是女职工人数的$\frac{2}{3}$.
(1)根据以上数据完成下面的2×2列联表.
(2)能否在犯错误的概率不超过0.001的前提下认为喜欢网购与职工性别有关系?
参考数据及公式:
K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.
(1)根据以上数据完成下面的2×2列联表.
| 喜欢网购 | 不喜欢网购 | 总计 | |
| 男职工 | |||
| 女职工 | |||
| 总计 |
参考数据及公式:
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
1.已知函数f(x)的图象是连续不断的,现给出x,f(x)的部分对应值如下表:
则函数f(x)一定有零点的区间是( )
| x | -2 | -1 | 1 | 2 | 3 |
| f(x) | -3 | -2 | 1 | 2 | 4 |
| A. | (1,2) | B. | (2,3) | C. | (-2,-1) | D. | (-1,1) |
11.若将字母o,o,r,t随机排列,则排得root的概率为( )
| A. | $\frac{1}{24}$ | B. | $\frac{1}{12}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{2}$ |
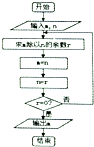 程序框图如图所示,若输入m,n的值分别为30,18,则程序框图中最后输出的m值等于6.
程序框图如图所示,若输入m,n的值分别为30,18,则程序框图中最后输出的m值等于6.