题目内容
14.针对时下的网购热,某单位对“喜欢网购与职工性别是否有关”进行了一次调查,其中男职工有60人,女职工人数是男职工人数的$\frac{1}{2}$,喜欢网购的男职工人数是男职工人数的$\frac{1}{6}$,喜欢网购的女职工人数是女职工人数的$\frac{2}{3}$.(1)根据以上数据完成下面的2×2列联表.
| 喜欢网购 | 不喜欢网购 | 总计 | |
| 男职工 | |||
| 女职工 | |||
| 总计 |
参考数据及公式:
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
分析 (1)本题是一个简单的数字的运算,根据a,b,c,d的已知和未知的结果,做出空格处的结果.
(2)由已知数据可求得观测值,把求得的观测值同临界值进行比较,看能否在犯错误的概率不超过0.001的前提下认为喜欢网购与职工性别有关系.
解答 解:(1)依题意,2×2列联表为:
| 喜欢网购 | 不喜欢网购 | 总计 | |
| 男职工 | 10 | 50 | 60 |
| 女职工 | 20 | 10 | 30 |
| 总计 | 30 | 60 | 90QUOTE |
(2)由K2=$\frac{90×(10×10-50×20)^{2}}{60×30×30×60}$=22.5≥10.828,…(10分)
因此,在犯错误的概率不超过0.001的前提下,认为喜欢网购与职工性别有关.…(12分)
点评 本题考查独立性检验的列联表.考查假设性判断,解题的过程比较麻烦,但这种问题的解答原理比较简单,是一个送分题目.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.在平行四边形ABCD中,E,F分别是BC,CD的中点,DE交AF于点G,记$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,则$\overrightarrow{AG}$=( )
| A. | $\frac{2}{5}$$\overrightarrow{a}$-$\frac{4}{5}$$\overrightarrow{b}$ | B. | $\frac{2}{5}$$\overrightarrow{a}$+$\frac{4}{5}$$\overrightarrow{b}$ | C. | -$\frac{2}{5}$$\overrightarrow{a}$+$\frac{4}{5}$$\overrightarrow{b}$ | D. | -$\frac{2}{5}$$\overrightarrow{a}$-$\frac{4}{5}$$\overrightarrow{b}$ |
9.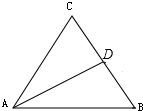 如图,在△ABC中,D为边BC的中点,则下列结论正确的是( )
如图,在△ABC中,D为边BC的中点,则下列结论正确的是( )
 如图,在△ABC中,D为边BC的中点,则下列结论正确的是( )
如图,在△ABC中,D为边BC的中点,则下列结论正确的是( )| A. | $\overrightarrow{AB}$+$\overrightarrow{AC}$=$\overrightarrow{AD}$ | B. | $\overrightarrow{AB}$-$\overrightarrow{AC}$=$\overrightarrow{BC}$ | C. | $\overrightarrow{AB}$+$\overrightarrow{DC}$=$\overrightarrow{AD}$ | D. | $\overrightarrow{AB}$-$\overrightarrow{DC}$=$\overrightarrow{BC}$ |
19.某校高一年级有200人,其中100人参加数学第二课堂活动.在期末考试中,分别对参加数学第二课堂活动的同学与未参加数学第二课堂活动的同学的数学成绩进行调查.按照学生数学成绩优秀与非优秀人数统计后,构成如下不完整的2×2列联表:
已知p是(1+2x)5展开式中的第三项系数,q是(1+2x)5展开式中的第四项的二项式系数.
(Ⅰ)求p与q的值;
(Ⅱ)请完成上面的2×2列联表,并判断若按99%的可靠性要求,能否认为“成绩优秀与参加数学第二课堂活动有关”.
| 优秀 | 非优秀 | 总计 | |
| 参加数学第二课堂活动 | p | ||
| 未参加数学第二课堂活动 | q | 100 | |
| 总计 | 200 |
(Ⅰ)求p与q的值;
(Ⅱ)请完成上面的2×2列联表,并判断若按99%的可靠性要求,能否认为“成绩优秀与参加数学第二课堂活动有关”.
6.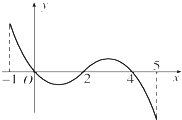 已知函数f(x)的定义域为[-1,5],f(x)的导函数f′(x)的图象如图所示.若f(x)在区间[m,m+1]上是单调函数,则实数m的取值范围是{m|m=-1或0≤m≤1或2≤m≤3或m=4}.
已知函数f(x)的定义域为[-1,5],f(x)的导函数f′(x)的图象如图所示.若f(x)在区间[m,m+1]上是单调函数,则实数m的取值范围是{m|m=-1或0≤m≤1或2≤m≤3或m=4}.
 已知函数f(x)的定义域为[-1,5],f(x)的导函数f′(x)的图象如图所示.若f(x)在区间[m,m+1]上是单调函数,则实数m的取值范围是{m|m=-1或0≤m≤1或2≤m≤3或m=4}.
已知函数f(x)的定义域为[-1,5],f(x)的导函数f′(x)的图象如图所示.若f(x)在区间[m,m+1]上是单调函数,则实数m的取值范围是{m|m=-1或0≤m≤1或2≤m≤3或m=4}.
3.已知两个实数a、b(a≠b)满足aea=beb,命题p:lna+a=lnb+b;命题q:(a+1)(b+1)<0.则下面命题是真命题的是( )
| A. | p∨(¬q) | B. | p∧(¬q) | C. | p∨q | D. | p∧q |