题目内容
18.已知α,β是两个不同的平面,m,n是两条不同的直线,现给出下列命题:①若m?α,n?α,m∥β,n∥β,则α∥β;
②若α⊥β,m?α,则m⊥β;
③若m⊥α,m∥β,则α⊥β;
④若m∥n,m?α,则n∥α.
其中正确命题的个数是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 利用线面平行、面面垂直线面垂直的性质定理和判定定理对四个难题分别分析解答.
解答 解:对于①,若m?α,n?α,m∥β,n∥β,根据面面平行的判定定理,如果直线m,n不相交,那么α与β不一定平行;故①错误;
对于②,若α⊥β,m?α,则m与β位置关系不确定;故②错误;
对于③,若m⊥α,m∥β,根据线面垂直的性质定理和面面垂直的判定定理可得α⊥β;故③正确;
对于④,若m∥n,m?α,则n∥α或者n?α;故④错误.
故选B.
点评 本题考查了线面平行、面面垂直线面垂直的性质定理和判定定理的运用,考查学生的空间想象能力;熟练运用定理是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
9.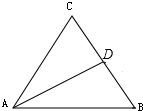 如图,在△ABC中,D为边BC的中点,则下列结论正确的是( )
如图,在△ABC中,D为边BC的中点,则下列结论正确的是( )
 如图,在△ABC中,D为边BC的中点,则下列结论正确的是( )
如图,在△ABC中,D为边BC的中点,则下列结论正确的是( )| A. | $\overrightarrow{AB}$+$\overrightarrow{AC}$=$\overrightarrow{AD}$ | B. | $\overrightarrow{AB}$-$\overrightarrow{AC}$=$\overrightarrow{BC}$ | C. | $\overrightarrow{AB}$+$\overrightarrow{DC}$=$\overrightarrow{AD}$ | D. | $\overrightarrow{AB}$-$\overrightarrow{DC}$=$\overrightarrow{BC}$ |
6.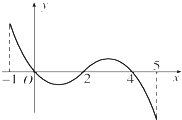 已知函数f(x)的定义域为[-1,5],f(x)的导函数f′(x)的图象如图所示.若f(x)在区间[m,m+1]上是单调函数,则实数m的取值范围是{m|m=-1或0≤m≤1或2≤m≤3或m=4}.
已知函数f(x)的定义域为[-1,5],f(x)的导函数f′(x)的图象如图所示.若f(x)在区间[m,m+1]上是单调函数,则实数m的取值范围是{m|m=-1或0≤m≤1或2≤m≤3或m=4}.
 已知函数f(x)的定义域为[-1,5],f(x)的导函数f′(x)的图象如图所示.若f(x)在区间[m,m+1]上是单调函数,则实数m的取值范围是{m|m=-1或0≤m≤1或2≤m≤3或m=4}.
已知函数f(x)的定义域为[-1,5],f(x)的导函数f′(x)的图象如图所示.若f(x)在区间[m,m+1]上是单调函数,则实数m的取值范围是{m|m=-1或0≤m≤1或2≤m≤3或m=4}.
3.已知两个实数a、b(a≠b)满足aea=beb,命题p:lna+a=lnb+b;命题q:(a+1)(b+1)<0.则下面命题是真命题的是( )
| A. | p∨(¬q) | B. | p∧(¬q) | C. | p∨q | D. | p∧q |
3.下列参数方程中,与普通方程x2+y-1=0等价的参数方程是( )
| A. | $\left\{{\begin{array}{l}{x=sinφ}\\{y={{cos}^2}φ}\end{array}}\right.$(φ为参数) | B. | $\left\{\begin{array}{l}{x=cosφ}\\{y=si{n}^{2}φ}\end{array}\right.$(φ为参数) | ||
| C. | $\left\{\begin{array}{l}{x=\sqrt{1-r}}\\{y=r}\end{array}\right.$(r为参数) | D. | $\left\{\begin{array}{l}{x=tanφ}\\{y=1-ta{n}^{2}φ}\end{array}\right.$(φ为参数) |
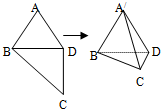 如图所示,在四边形ABCD中,AB=AD=CD=1,BD=$\sqrt{2}$,BD⊥CD,将四边形ABCD沿对角线BD折成四面体A′-BCD,使平面A′BD⊥平面BCD,则下列结论正确的是(2)(4).
如图所示,在四边形ABCD中,AB=AD=CD=1,BD=$\sqrt{2}$,BD⊥CD,将四边形ABCD沿对角线BD折成四面体A′-BCD,使平面A′BD⊥平面BCD,则下列结论正确的是(2)(4).