题目内容
1.已知函数f(x)的图象是连续不断的,现给出x,f(x)的部分对应值如下表:| x | -2 | -1 | 1 | 2 | 3 |
| f(x) | -3 | -2 | 1 | 2 | 4 |
| A. | (1,2) | B. | (2,3) | C. | (-2,-1) | D. | (-1,1) |
分析 由所给的函数值的表格可以看出,在x=-1与x=1这两个数字对应的函数值的符号不同,即f(-1)f(1)<0,根据零点判定定理看出零点的位置.
解答 解:由所给的函数值的表格可以看出,
在x=-1与x=1这两个数字对应的函数值的符号不同,
即f(-1)f(1)<0,
∴函数的零点在(-1,1)上,
故选:D.
点评 本题考查函数的零点的判定定理,是一个基础题,解题的关键是看清那两个函数值之间符号不同,这里不用运算,只要仔细观察即可.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
12.设集合A={1,2,3},B={2,3,4},C⊆A∩B,则集合C可能是( )
| A. | {1,2} | B. | {1,3} | C. | {2,3} | D. | {2,4} |
9.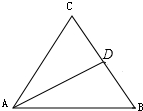 如图,在△ABC中,D为边BC的中点,则下列结论正确的是( )
如图,在△ABC中,D为边BC的中点,则下列结论正确的是( )
 如图,在△ABC中,D为边BC的中点,则下列结论正确的是( )
如图,在△ABC中,D为边BC的中点,则下列结论正确的是( )| A. | $\overrightarrow{AB}$+$\overrightarrow{AC}$=$\overrightarrow{AD}$ | B. | $\overrightarrow{AB}$-$\overrightarrow{AC}$=$\overrightarrow{BC}$ | C. | $\overrightarrow{AB}$+$\overrightarrow{DC}$=$\overrightarrow{AD}$ | D. | $\overrightarrow{AB}$-$\overrightarrow{DC}$=$\overrightarrow{BC}$ |
16.曲线y=x3在点x=2处的切线方程是( )
| A. | 12x-y-16=0 | B. | 12x+y-32=0 | C. | 4x-y=0 | D. | 4x+y-16=0 |
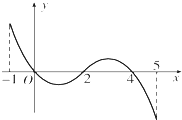 已知函数f(x)的定义域为[-1,5],f(x)的导函数f′(x)的图象如图所示.若f(x)在区间[m,m+1]上是单调函数,则实数m的取值范围是{m|m=-1或0≤m≤1或2≤m≤3或m=4}.
已知函数f(x)的定义域为[-1,5],f(x)的导函数f′(x)的图象如图所示.若f(x)在区间[m,m+1]上是单调函数,则实数m的取值范围是{m|m=-1或0≤m≤1或2≤m≤3或m=4}.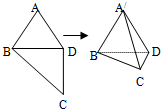 如图所示,在四边形ABCD中,AB=AD=CD=1,BD=$\sqrt{2}$,BD⊥CD,将四边形ABCD沿对角线BD折成四面体A′-BCD,使平面A′BD⊥平面BCD,则下列结论正确的是(2)(4).
如图所示,在四边形ABCD中,AB=AD=CD=1,BD=$\sqrt{2}$,BD⊥CD,将四边形ABCD沿对角线BD折成四面体A′-BCD,使平面A′BD⊥平面BCD,则下列结论正确的是(2)(4).