题目内容
17. 程序框图如图所示,若输入m,n的值分别为30,18,则程序框图中最后输出的m值等于6.
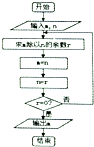
程序框图如图所示,若输入m,n的值分别为30,18,则程序框图中最后输出的m值等于6.
分析 模拟执行程序框图,依次写出每次循环得到的结果,当r=0,m=6,n=0时满足条件r=0,退出循环,输出m的值为6.
解答 解:模拟执行程序框图,依次写出每次循环得到的结果如下:
m=30,n=18,r=12
m=18,n=12,不满足条件r=0,r=6
m=12,n=6,不满足条件r=0,r=0
m=6,n=0,满足条件r=0,退出循环,输出m的值为6,结束.
故答案为:6.
点评 本题主要考查了循环结构的程序框图,正确依次写出每次循环得到的结果是解题的关键,属于基础题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
7.f(x),g(x)分别是定义在R上的奇函数和偶函数,当x<0时,f′(x)g(x)+f(x)g′(x)>0,且g(-3)=0,则不等式f(x)g(x)<0的解集是( )
| A. | (-∞,-3)∪(0,3) | B. | (-∞,-3)∪(3,+∞) | C. | (-3,0)∪(3,+∞) | D. | (-3,0)∪(0,3) |
12.设集合A={1,2,3},B={2,3,4},C⊆A∩B,则集合C可能是( )
| A. | {1,2} | B. | {1,3} | C. | {2,3} | D. | {2,4} |
2.在平行四边形ABCD中,E,F分别是BC,CD的中点,DE交AF于点G,记$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,则$\overrightarrow{AG}$=( )
| A. | $\frac{2}{5}$$\overrightarrow{a}$-$\frac{4}{5}$$\overrightarrow{b}$ | B. | $\frac{2}{5}$$\overrightarrow{a}$+$\frac{4}{5}$$\overrightarrow{b}$ | C. | -$\frac{2}{5}$$\overrightarrow{a}$+$\frac{4}{5}$$\overrightarrow{b}$ | D. | -$\frac{2}{5}$$\overrightarrow{a}$-$\frac{4}{5}$$\overrightarrow{b}$ |
9.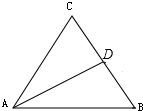 如图,在△ABC中,D为边BC的中点,则下列结论正确的是( )
如图,在△ABC中,D为边BC的中点,则下列结论正确的是( )
 如图,在△ABC中,D为边BC的中点,则下列结论正确的是( )
如图,在△ABC中,D为边BC的中点,则下列结论正确的是( )| A. | $\overrightarrow{AB}$+$\overrightarrow{AC}$=$\overrightarrow{AD}$ | B. | $\overrightarrow{AB}$-$\overrightarrow{AC}$=$\overrightarrow{BC}$ | C. | $\overrightarrow{AB}$+$\overrightarrow{DC}$=$\overrightarrow{AD}$ | D. | $\overrightarrow{AB}$-$\overrightarrow{DC}$=$\overrightarrow{BC}$ |
6.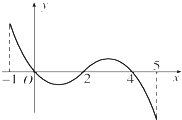 已知函数f(x)的定义域为[-1,5],f(x)的导函数f′(x)的图象如图所示.若f(x)在区间[m,m+1]上是单调函数,则实数m的取值范围是{m|m=-1或0≤m≤1或2≤m≤3或m=4}.
已知函数f(x)的定义域为[-1,5],f(x)的导函数f′(x)的图象如图所示.若f(x)在区间[m,m+1]上是单调函数,则实数m的取值范围是{m|m=-1或0≤m≤1或2≤m≤3或m=4}.
 已知函数f(x)的定义域为[-1,5],f(x)的导函数f′(x)的图象如图所示.若f(x)在区间[m,m+1]上是单调函数,则实数m的取值范围是{m|m=-1或0≤m≤1或2≤m≤3或m=4}.
已知函数f(x)的定义域为[-1,5],f(x)的导函数f′(x)的图象如图所示.若f(x)在区间[m,m+1]上是单调函数,则实数m的取值范围是{m|m=-1或0≤m≤1或2≤m≤3或m=4}.
3.下列参数方程中,与普通方程x2+y-1=0等价的参数方程是( )
| A. | $\left\{{\begin{array}{l}{x=sinφ}\\{y={{cos}^2}φ}\end{array}}\right.$(φ为参数) | B. | $\left\{\begin{array}{l}{x=cosφ}\\{y=si{n}^{2}φ}\end{array}\right.$(φ为参数) | ||
| C. | $\left\{\begin{array}{l}{x=\sqrt{1-r}}\\{y=r}\end{array}\right.$(r为参数) | D. | $\left\{\begin{array}{l}{x=tanφ}\\{y=1-ta{n}^{2}φ}\end{array}\right.$(φ为参数) |