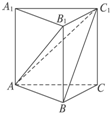
题目内容
在正方体ABCD-A1B1C1D1中,AA1=4,G为BB1的中点,则点G到平面A1BCD1的距离为( )
A.2
| B.2 | C.
| D.1 |
∵B1B∩平面A1BCD1=B,G为BB1的中点,点G到平面A1BCD1的距离等于B1到平面A1BCD1的距离的一半.
过B1在平面AA1B1B内作B1H⊥A1B,则H为A1B中点.又因为D1A1⊥平面AA1B1B,所以D1A1⊥B1H,D1A1∩A1B=A1B,∴B1H⊥平面A1BCD1,
正方体棱长为4,所以B1H=
×4
=2
,点G到平面A1BCD1的距离为
.
故选C
过B1在平面AA1B1B内作B1H⊥A1B,则H为A1B中点.又因为D1A1⊥平面AA1B1B,所以D1A1⊥B1H,D1A1∩A1B=A1B,∴B1H⊥平面A1BCD1,
正方体棱长为4,所以B1H=
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |
故选C

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 中,
中,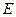 ,
,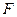 分别是
分别是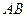 ,
,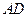 的中点.
的中点.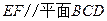 .
.
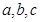 为直线,
为直线,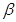 为平面,给出下列命题
为平面,给出下列命题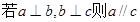 ②
②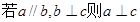
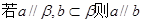 ④
④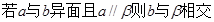
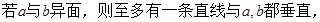 其中真命题的个数是( )
其中真命题的个数是( )