题目内容
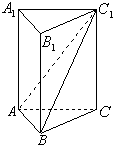
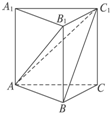
如图,在直三棱柱ABC-A1B1C1中,AB1⊥BC1,AB=CC1=1,BC=2.
(1)求证:A1C1⊥AB;
(2)求点B1到平面ABC1的距离.
(1)求证:A1C1⊥AB;
(2)求点B1到平面ABC1的距离.

(1)证明:连接A1B,则A1B⊥AB1.
又∵AB1⊥BC1,
∴AB1⊥平面A1BC1.
∴AB1⊥A1C1.
又∵A1C1⊥BB1,
∴A1C1⊥平面ABB1.
∴A1C1⊥AB.
(2)由(1)知AB⊥AC,∵AB⊥AC1,
又∵AB=1,BC=2,
∴AC=
,AC1=2.
∴S△ABC1=1.
设所求距离为d,
∴VB1-ABC1=VC1-ABB1.
∴
S△ABC1•d=
S△ABB1•A1C1.
∴
•1•d=
•
•
.
∴d=
.点B1到平面ABC1的距离d=
.
又∵AB1⊥BC1,
∴AB1⊥平面A1BC1.
∴AB1⊥A1C1.
又∵A1C1⊥BB1,
∴A1C1⊥平面ABB1.
∴A1C1⊥AB.
(2)由(1)知AB⊥AC,∵AB⊥AC1,
又∵AB=1,BC=2,
∴AC=
| 3 |
∴S△ABC1=1.
设所求距离为d,
∴VB1-ABC1=VC1-ABB1.
∴
| 1 |
| 3 |
| 1 |
| 3 |
∴
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
∴d=
| ||
| 2 |
| ||
| 2 |

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案
相关题目