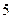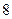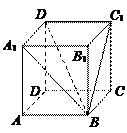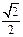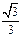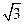题目内容
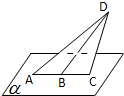
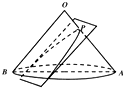
如图，已知圆锥的底面直径和母线长均为4，过OA上一点P作平面α，当OB∥α时平面a截圆锥所得的截口曲线为抛物线，设抛物线的焦点为F，若OP=1，则|PF|长为（ ）
A．
| B．
| C．1 | D．2 |
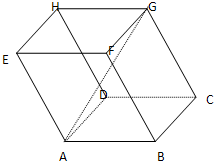
如图1所示
设抛物线与圆锥底面交点为C、D，连结CD交AB于点E，
连结PE，则PE∥OB且点F在PE上，连结BC、AC
∵正△OAB中，PE∥OB
∴△PAE是正三角形，边长AE=AP=4-1=3
∵AB是底面圆的直径，CE⊥AB于E
∴CE2=BE•AE=3，可得CE=
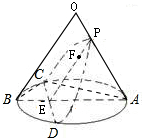
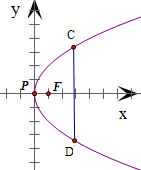
图1 图2
在平面α内，以P为原点，PF所在直线为x轴建立如图2所示直角坐标系
设抛物线的方程为y2=2px（p＞0）
由C点坐标（3，
），得（
）2=2p•3，所以p=
因此，|PF|长为
=
，
故答案为：
设抛物线与圆锥底面交点为C、D，连结CD交AB于点E，
连结PE，则PE∥OB且点F在PE上，连结BC、AC
∵正△OAB中，PE∥OB
∴△PAE是正三角形，边长AE=AP=4-1=3
∵AB是底面圆的直径，CE⊥AB于E
∴CE2=BE•AE=3，可得CE=
| 3 |
图1 图2
在平面α内，以P为原点，PF所在直线为x轴建立如图2所示直角坐标系
设抛物线的方程为y2=2px（p＞0）
由C点坐标（3，
| 3 |
| 3 |
| 1 |
| 2 |
因此，|PF|长为
| p |
| 2 |
| 1 |
| 4 |
故答案为：
| 1 |
| 4 |
练习册系列答案
新活力总动员暑系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
，
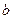是异面直线，
，
，
，
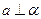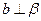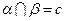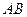是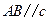
．
