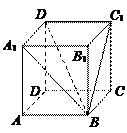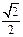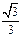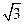题目内容
已知正四面体ABCD的棱长为a.
(1)求证:AC⊥BD
(2)求AC与BD的距离.
(3)求它的内切球的半径.
(1)求证:AC⊥BD
(2)求AC与BD的距离.
(3)求它的内切球的半径.
(1)证明:取AC中点E
∵AD=DC,AB=BC
∴AC⊥DE,AC⊥BE
∴AC⊥平面BDE
∴AC⊥BD
(2)取BD中点F,则,EF⊥BD
同理可证EF⊥AC
∴EF为AC与BD的距离
∵正四面体ABCD的棱长为a
∴DE=
a
∴EF=
a
(3)设内切球心为O,半径为r
∵VA-BCD=VO-ABC+VO-PAB+VO=PBC+VO-PAC
∴r=
a
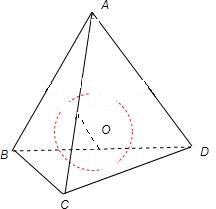
∵AD=DC,AB=BC
∴AC⊥DE,AC⊥BE
∴AC⊥平面BDE
∴AC⊥BD
(2)取BD中点F,则,EF⊥BD
同理可证EF⊥AC
∴EF为AC与BD的距离
∵正四面体ABCD的棱长为a
∴DE=
| ||
| 2 |
∴EF=
| ||
| 2 |
(3)设内切球心为O,半径为r
∵VA-BCD=VO-ABC+VO-PAB+VO=PBC+VO-PAC
∴r=
| ||
| 12 |


练习册系列答案
相关题目
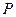 点是
点是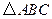 所在平面外一点,若
所在平面外一点,若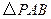 是锐角三角形且
是锐角三角形且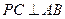 .
.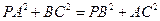 .
.