题目内容
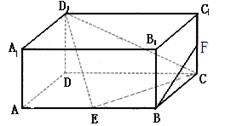
如图,在棱长为2的正方体ABCD -A1B1C1D1中,点O是底面ABCD的中心,点E,F分别是CC1,AD的中点,则异面直线OE与FD1所成角的余弦值为 .


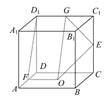
取D1C1的中点G,连接OF,OG,GE.
因为点O是底面ABCD的中心,F为AD的中点,
所以OF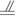
 CD,D1G
CD,D1G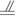
 CD,即OF
CD,即OF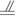 D1G.
D1G.
所以四边形OGD1F为平行四边形.所以D1F∥GO,即OE与FD1所成角也就是OE与OG所成角.
在△OGE中,OG=FD1=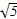 ,GE=
,GE=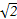 ,OE=
,OE=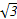 ,
,
所以GE2+OE2=OG2,即△GOE为直角三角形,所以cos∠GOE=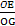 =
=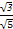 =
=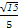 .
.
异面直线OE与FD1所成角的余弦值为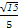 .
.

因为点O是底面ABCD的中心,F为AD的中点,
所以OF
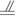
 CD,D1G
CD,D1G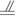
 CD,即OF
CD,即OF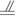 D1G.
D1G.所以四边形OGD1F为平行四边形.所以D1F∥GO,即OE与FD1所成角也就是OE与OG所成角.
在△OGE中,OG=FD1=
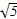 ,GE=
,GE=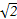 ,OE=
,OE=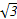 ,
,所以GE2+OE2=OG2,即△GOE为直角三角形,所以cos∠GOE=
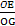 =
=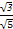 =
=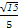 .
.异面直线OE与FD1所成角的余弦值为
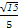 .
.
练习册系列答案
相关题目
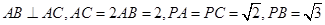 .
.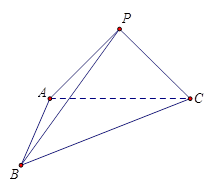
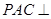 平面
平面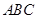 ;
;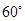 的角?若存在,求BQ的长;若不存在,请说明理由.
的角?若存在,求BQ的长;若不存在,请说明理由.
 中,
中, 分别是
分别是 的中点.则直线
的中点.则直线 和
和 所成的角为__________.
所成的角为__________.
 ,则二面角
,则二面角 的大小为( )
的大小为( )




 ,底面边长为
,底面边长为 ,E为SA的中点,则异面直线BE和SC所成的角为( ).
,E为SA的中点,则异面直线BE和SC所成的角为( ).
 沿对角线
沿对角线 折成一个直二面角,点
折成一个直二面角,点 到达点
到达点 ,则异面直线
,则异面直线 与
与 所成角是( )
所成角是( )
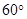


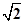 ,CD=CB=
,CD=CB=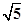 ,且
,且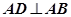 ,现将
,现将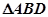 沿着对角线BD翻折成
沿着对角线BD翻折成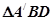 ,则在
,则在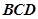 内的过程中,直线
内的过程中,直线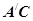 与平面
与平面