题目内容
如图,在长方体ABCD—A1B1C1D1中,AD=AA1=1,AB=2,E为AB的中点,F为CC1的中点.
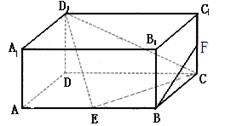
(1)证明:B F//平面E CD1
(2)求二面角D1—EC—D的余弦值.

(1)证明:B F//平面E CD1
(2)求二面角D1—EC—D的余弦值.
(1)证明:取CD1中点G,连结FG得出 且FG //BE;
且FG //BE;
由四边形FG EB为平行四边形得到BF //GE,证得B F//平面E CD1;
(2)cos∠DED1 .
.
 且FG //BE;
且FG //BE;由四边形FG EB为平行四边形得到BF //GE,证得B F//平面E CD1;
(2)cos∠DED1
 .
.试题分析:(1)证明:取CD1中点G,连结FG
∵F为CC1的中点.D1 ∴
 且FG //C1D1
且FG //C1D1∵
 且AB //C1D1∴
且AB //C1D1∴ 且FG //BE
且FG //BE∴四边形FG EB为平行四边形∴BF //GE 4分
∵
 平面E CD1
平面E CD1  平面E CD1
平面E CD1 ∴B F//平面E CD1 7分
(2)连结DE
∵AD=AA1=1,AB="2" , E为AB的中点
∴
 9分
9分∵
 平面ABCD ∴
平面ABCD ∴ E C
E C又

 平面E DD1
平面E DD1  平面E DD1
平面E DD1∴
 平面E DD1
平面E DD1∴
 E D1 11分
E D1 11分∴∠DED1为二面角D1—EC—D的平面角. 12分
 中
中 ∴
∴ 中
中
∴cos∠DED1
 14分
14分点评:中档题,立体几何题,是高考必考内容,往往涉及垂直关系、平行关系、角、距离、体积的计算。在计算问题中,有“几何法”和“向量法”。利用几何法,要遵循“一作、二证、三计算”的步骤。解题过程中,注意转化成平面几何问题,是解决立体几何问题的一个基本思路。

练习册系列答案
相关题目

 中,直线
中,直线 和平面
和平面 所成角的余弦值大小为( )
所成角的余弦值大小为( )



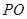 中,已知
中,已知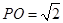 ,⊙O的直径
,⊙O的直径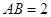 ,
,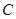 是
是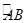 的中点,
的中点,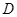 为
为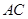 的中点.
的中点.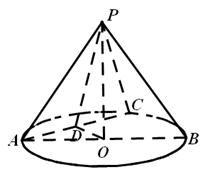
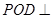 平面
平面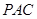 ;
;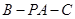 的余弦值.
的余弦值.  是直三棱柱,
是直三棱柱, 为直角,点
为直角,点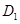 、
、 分别是
分别是 、
、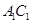 的中点,若
的中点,若 ,则
,则 与
与 所成角的余弦值是( )
所成角的余弦值是( )






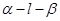 的大小是60°,线段
的大小是60°,线段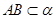 .
.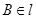 ,
,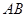 与
与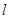 所成的角为30°.则
所成的角为30°.则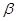 所成的角的正弦值是 .
所成的角的正弦值是 .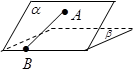
 中,
中, 分别是
分别是 的中点,若
的中点,若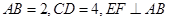 ,则
,则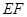 与
与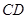 所成的角的度数为( )
所成的角的度数为( )


