题目内容
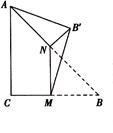
如图，在正方体ABCD-A1B1C1D1中，M、N、P分别是C1C、B1C1、C1D1的中点，求证：
（1）AP⊥MN；
（2）平面MNP∥平面A1BD．
（1）AP⊥MN；
（2）平面MNP∥平面A1BD．
证明：（1）连接BC1、B1C，则B1C⊥BC1，BC1是AP在面BB1C1C上的射影．∴AP⊥B1C．
又B1C∥MN，∴AP⊥MN．
（2）连接B1D1，∵P、N分别是D1C1、B1C1的中点，
∴PN∥B1D1．又B1D1∥BD，
∴PN∥BD．又PN不在平面A1BD上，
∴PN∥平面A1BD．
同理，MN∥平面A1BD．又PN∩MN=N，
∴平面PMN∥平面A1BD．
又B1C∥MN，∴AP⊥MN．
（2）连接B1D1，∵P、N分别是D1C1、B1C1的中点，
∴PN∥B1D1．又B1D1∥BD，
∴PN∥BD．又PN不在平面A1BD上，
∴PN∥平面A1BD．
同理，MN∥平面A1BD．又PN∩MN=N，
∴平面PMN∥平面A1BD．
练习册系列答案
相关题目
，
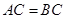，M、N分别是BC、AB的中点，沿直线MN将折起，使二面角
的大小为
，则
与平面ABC所成角的正切值为（ ）
B.
C.
D.
