题目内容
将正方形 沿对角线
沿对角线 折成一个直二面角,点
折成一个直二面角,点 到达点
到达点 ,则异面直线
,则异面直线 与
与 所成角是( )
所成角是( )
 沿对角线
沿对角线 折成一个直二面角,点
折成一个直二面角,点 到达点
到达点 ,则异面直线
,则异面直线 与
与 所成角是( )
所成角是( )A. | B.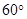 | C. | D. |
B
试题分析:方法一:如图,则
 所以
所以 与
与 所成的角即为异面直线
所成的角即为异面直线 与
与 所成角,设正方形边长为2,则
所成角,设正方形边长为2,则 ,所以
,所以 为等边三角形,故异面直线
为等边三角形,故异面直线 与
与 所成角是
所成角是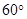 .
.方法二:建立如图所示的空间坐标系,则

所以
 ,
,所以
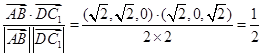 ,
,故异面直线
 与
与 所成角是
所成角是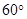 .
.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目

 =1.
=1.
 ?若存在,求出CM的长;若不存在,请说明理由.
?若存在,求出CM的长;若不存在,请说明理由. .
.

 中,直线
中,直线 和平面
和平面 所成角的余弦值大小为( )
所成角的余弦值大小为( )



