题目内容
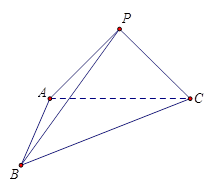
(15分)在三棱锥P-ABC中,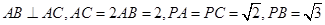 .
.
(1)求证:平面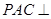 平面
平面 ;
;
(2)求BC与平面PAB所成角的正弦值;
(3)在棱BC上是否存在点Q使得AQ与PC成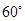 的角?若存在,求BQ的长;若不存在,请说明理由.
的角?若存在,求BQ的长;若不存在,请说明理由.
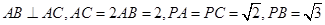 .
.
(1)求证:平面
 平面
平面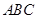 ;
;(2)求BC与平面PAB所成角的正弦值;
(3)在棱BC上是否存在点Q使得AQ与PC成
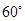 的角?若存在,求BQ的长;若不存在,请说明理由.
的角?若存在,求BQ的长;若不存在,请说明理由.(1)见解析(2) (3)见解析
(3)见解析
 (3)见解析
(3)见解析(1)证明:由题意得:
 ,又
,又 ,所以
,所以 平面
平面 ,所以平面
,所以平面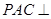 平面
平面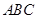 5分
5分(2)解:法一、由(1)得
 平面
平面 ,所以
,所以
 ,又
,又 ,所以
,所以 平面
平面 ,所以PB是直线BC在平面PAB内的射影,所以
,所以PB是直线BC在平面PAB内的射影,所以 就是直线BC与平面PAB所成的角,易得
就是直线BC与平面PAB所成的角,易得 10分
10分法二、建立空间直角坐标系,利用空间向量求解.
(3)法一、设
 ,则
,则 ,
, ,
,又
 ,所以
,所以 ,所以
,所以 即
即 15分
15分【考点定位】本题考查空间面面垂直、直线与直线所成的角及异面直线所成的角,考查空间向量的运算,意在考查学生的空间想象能力、逻辑推理能力及运算能力.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目

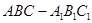 中,
中,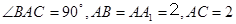 ,
,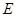 为
为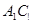 中点,求直线
中点,求直线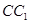 与平面
与平面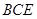 所成角的大小.(结果用反三角函数值表示)
所成角的大小.(结果用反三角函数值表示)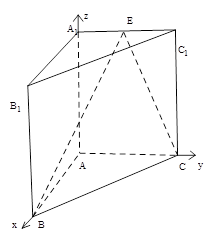
 中,
中, ,
,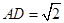 ,且
,且 ,以BD为折线,把△ABD折起,
,以BD为折线,把△ABD折起, ,连接AC.
,连接AC.

 中,直线
中,直线 和平面
和平面 所成角的余弦值大小为( )
所成角的余弦值大小为( )



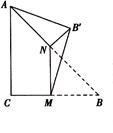
 ,
,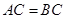 ,M、N分别是BC、AB的中点,沿直线MN将折起,使二面角
,M、N分别是BC、AB的中点,沿直线MN将折起,使二面角 的大小为
的大小为 ,则
,则 与平面ABC所成角的正切值为( )
与平面ABC所成角的正切值为( ) B.
B. C.
C. D.
D.