题目内容
13.已知命题p:实数t满足t2-5at+4a2<0(其中a≠0),命题q:方程$\frac{{x}^{2}}{t-2}+\frac{{y}^{2}}{t-6}=1$表示双曲线(1)若a=1,且p∧q为真命题,求实数t的取值范围;
(2)若p是q的必要不充分条件,求实数a的取值范围.
分析 (1)若a=1,分别求出p,q成立的等价条件,利用p∧q为真命题,即可求实数t的取值范围;
(2)利用p是q的充分不必要条件,求实数a的取值范围.
解答 解:(1)若a=1,则不等式为t2-5t+4<0,即1<t<4,
p:t∈(1,4),
若方程$\frac{{x}^{2}}{t-2}+\frac{{y}^{2}}{t-6}=1$=1表示双曲线,
则(t-2)(t-6)<0,即2<t<6.
q:t∈(2,6),
若p∧q为真命题,则p,q都为真命题,
即$\left\{\begin{array}{l}{1<t<4}\\{2<t<6}\end{array}\right.$,解得2<t<4,
则实数t的取值范围{t|2<t<4}.
(2)若t2-5at+4a2<0(其中a≠0),
则(t-a)(t-4a)<0,
若a>0,则得a<t<4a,
若a<0,则4a<t<a,
∵q:t∈(2,6),
∴若p是q的必要不充分条件,
则当a>0时,$\left\{\begin{array}{l}{4a≥6}\\{a≤2}\end{array}\right.$,即$\left\{\begin{array}{l}{a≥\frac{3}{2}}\\{a≤2}\end{array}\right.$,解得$\frac{3}{2}$≤a≤2,
若a<0,则不满足条件.
即实数a的取值范围是[$\frac{3}{2}$,2].
点评 本题主要考查复合命题与简单命题之间的关系,利用充分条件和必要条件的定义是解决本题的关键,

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.若复数z满足z=$\frac{2i}{1-i}$,则在复平面内,z对应的点坐标是( )
| A. | (-1,1) | B. | (-1,-1) | C. | (1,-1) | D. | (1,1) |
1.设二次函数f(x)=x2+bx+c(b,c∈R)的导函数为f′(x),关于x的方程f(x)=f′(x)有两个相等 实根,则$\frac{{b}^{2}}{1+{c}^{2}}$的最大值为( )
| A. | 2$\sqrt{2}$-2 | B. | 2$\sqrt{2}$+2 | C. | $\frac{1}{2}$ | D. | 1 |
8.已知x>0,y>0,且2x+y=1,则$\frac{1}{x}+\frac{1}{y}$的最小值是( )
| A. | 6 | B. | 4$\sqrt{2}$ | C. | 3+2$\sqrt{2}$ | D. | 3+4$\sqrt{2}$ |
18.双曲线9x2-4y2=36的渐近线方程是( )
| A. | y=$±\frac{3}{2}x$ | B. | y=$±\frac{2}{3}x$ | C. | y=$±\frac{9}{4}x$ | D. | y=$±\frac{4}{9}x$ |
5.一个几何体的三视图如图所示,则该几何体可以是( )
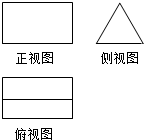

| A. | 棱锥 | B. | 棱台 | C. | 圆锥 | D. | 棱柱 |