题目内容
4．若复数z满足z=$\frac{2i}{1-i}$，则在复平面内，z对应的点坐标是（ ）| A． | （-1，1） | B． | （-1，-1） | C． | （1，-1） | D． | （1，1） |
分析 直接由复数代数形式的乘除运算化简复数z，则在复平面内，z对应的点坐标可求．
解答 解：由z=$\frac{2i}{1-i}$=$\frac{2i（1+i）}{（1-i）（1+i）}=\frac{-2+2i}{2}=-1+i$，
则在复平面内，z对应的点坐标是：（-1，1）．
故选：A．
点评 本题考查了复数代数形式的乘除运算，考查了复数的代数表示法及其几何意义，是基础题．
练习册系列答案
相关题目
14．若曲线C上的点到椭圆 $\frac{{x}^{2}}{1{3}^{2}}$+$\frac{{y}^{2}}{1{2}^{2}}$=1的两个焦点的距离的差的绝对值等于8，则曲线C的标准方程为（ ）
| A． | $\frac{{x}^{2}}{1{3}^{2}}$-$\frac{{y}^{2}}{1{2}^{2}}$=1 | B． | $\frac{{x}^{2}}{1{3}^{2}}$-$\frac{{y}^{2}}{{5}^{2}}$=1 | ||
| C． | $\frac{{x}^{2}}{{3}^{2}}$-$\frac{{y}^{2}}{{4}^{2}}$=1 | D． | $\frac{{x}^{2}}{{4}^{2}}$-$\frac{{y}^{2}}{{3}^{2}}$=1 |
15．
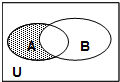已知全集U=R，集合A={x|x＞1}，集合B={x|3x-4≤0}，满足如图所示的阴影部分的集合是（ ）
已知全集U=R，集合A={x|x＞1}，集合B={x|3x-4≤0}，满足如图所示的阴影部分的集合是（ ）| A． | {x|x＞1} | B． | {x|1＜x≤$\frac{4}{3}$} | C． | {x|x≤1} | D． | {x|x＞$\frac{4}{3}$} |
12．已知F1，F2是椭圆上的两个焦点，过F1且与椭圆长轴垂直的直线交椭圆于A，B两点，若△ABF2是正三角形，则这个椭圆的离心率是（ ）
| A． | $\frac{\sqrt{3}}{2}$ | B． | $\frac{\sqrt{3}}{3}$ | C． | $\frac{\sqrt{2}}{2}$ | D． | $\frac{\sqrt{2}}{3}$ |
9．阅读程序图，该程序图输出的结果是（ ）
| A． | 94 | B． | 92 | C． | 95 | D． | 93 |