题目内容
3.已知函数f(x)=$\sqrt{{{log}_2}(x-1)}$的定义域为A,B={y|y=($\frac{1}{2}$)x,-4≤x≤0}.(Ⅰ)求A∩B;
(Ⅱ)若C={x|m-6≤x≤4m}且B⊆C,求m的取值范围.
分析 (Ⅰ)由题意得log2(x-1)≥0,从而解出集合A,再化简集合B,从而求交集;
(Ⅱ)结合(I)知C={x|m-6≤x≤4m},B=[1,16],且B⊆C;从而可得$\left\{\begin{array}{l}{m-6≤1}\\{4m≥16}\end{array}\right.$,从而解得.
解答 解:(Ⅰ)由题意得,log2(x-1)≥0,
故x≥2;
故A=[2,+∞),
∵-4≤x≤0,
∴1≤($\frac{1}{2}$)x≤16,
故B=[1,16],
故A∩B=[2,16];
(Ⅱ)∵C={x|m-6≤x≤4m},B=[1,16],且B⊆C,
∴$\left\{\begin{array}{l}{m-6≤1}\\{4m≥16}\end{array}\right.$,
解得,4≤m≤7.
点评 本题考查了函数的定义域与值域的求法及集合的运算与集合关系的应用,属于基础题.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
14.若曲线C上的点到椭圆 $\frac{{x}^{2}}{1{3}^{2}}$+$\frac{{y}^{2}}{1{2}^{2}}$=1的两个焦点的距离的差的绝对值等于8,则曲线C的标准方程为( )
| A. | $\frac{{x}^{2}}{1{3}^{2}}$-$\frac{{y}^{2}}{1{2}^{2}}$=1 | B. | $\frac{{x}^{2}}{1{3}^{2}}$-$\frac{{y}^{2}}{{5}^{2}}$=1 | ||
| C. | $\frac{{x}^{2}}{{3}^{2}}$-$\frac{{y}^{2}}{{4}^{2}}$=1 | D. | $\frac{{x}^{2}}{{4}^{2}}$-$\frac{{y}^{2}}{{3}^{2}}$=1 |
11.如图,在公路MN的两侧有四个村镇:A1、B1、C1、D1通过小路和公路相连,各路口分别是A、B、C、D,现要在公路上建一个长途汽车站,为使各村镇村民到汽车站所走的路程总和最小,汽车站应建在( )
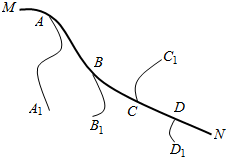

| A. | A处 | B. | D处 | ||
| C. | B、C间的任何一处(包括B、C) | D. | A、B之间的任何一处(包括A、B) |
18.由函数y=lg(1-2x)的图象得到函数y=lg(3-2x)的图象,只需要( )
| A. | 向左平移1个单位 | B. | 向右平移1个单位 | C. | 向左平移2个单位 | D. | 向右平移2个单位 |
15.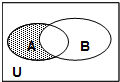 已知全集U=R,集合A={x|x>1},集合B={x|3x-4≤0},满足如图所示的阴影部分的集合是( )
已知全集U=R,集合A={x|x>1},集合B={x|3x-4≤0},满足如图所示的阴影部分的集合是( )
 已知全集U=R,集合A={x|x>1},集合B={x|3x-4≤0},满足如图所示的阴影部分的集合是( )
已知全集U=R,集合A={x|x>1},集合B={x|3x-4≤0},满足如图所示的阴影部分的集合是( )| A. | {x|x>1} | B. | {x|1<x≤$\frac{4}{3}$} | C. | {x|x≤1} | D. | {x|x>$\frac{4}{3}$} |
12.已知F1,F2是椭圆上的两个焦点,过F1且与椭圆长轴垂直的直线交椭圆于A,B两点,若△ABF2是正三角形,则这个椭圆的离心率是( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{2}}{3}$ |
 如图,在△ABC中,|$\overrightarrow{AB}$|=4,|$\overrightarrow{AC}$|=2,∠BAC=90°,D,E,F分别是边BC,CA,AB上的点且$\overrightarrow{CE}$=$\frac{1}{4}\overrightarrow{CA}$,$\overrightarrow{AF}$=$\frac{1}{4}\overrightarrow{AB}$,$\overrightarrow{BD}$=$\frac{1}{4}\overrightarrow{BC}$,则$\overrightarrow{DE}$•$\overrightarrow{DF}$的值为$\frac{11}{2}$.
如图,在△ABC中,|$\overrightarrow{AB}$|=4,|$\overrightarrow{AC}$|=2,∠BAC=90°,D,E,F分别是边BC,CA,AB上的点且$\overrightarrow{CE}$=$\frac{1}{4}\overrightarrow{CA}$,$\overrightarrow{AF}$=$\frac{1}{4}\overrightarrow{AB}$,$\overrightarrow{BD}$=$\frac{1}{4}\overrightarrow{BC}$,则$\overrightarrow{DE}$•$\overrightarrow{DF}$的值为$\frac{11}{2}$.