题目内容
8.已知x>0,y>0,且2x+y=1,则$\frac{1}{x}+\frac{1}{y}$的最小值是( )| A. | 6 | B. | 4$\sqrt{2}$ | C. | 3+2$\sqrt{2}$ | D. | 3+4$\sqrt{2}$ |
分析 由题意可得$\frac{1}{x}+\frac{1}{y}$=($\frac{1}{x}+\frac{1}{y}$)(2x+y)=3+$\frac{y}{x}$+$\frac{2x}{y}$,由基本不等式求最值可得.
解答 解:∵x>0,y>0,且2x+y=1,
∴$\frac{1}{x}+\frac{1}{y}$=($\frac{1}{x}+\frac{1}{y}$)(2x+y)
=3+$\frac{y}{x}$+$\frac{2x}{y}$≥3+2$\sqrt{\frac{y}{x}•\frac{2x}{y}}$=3+2$\sqrt{2}$
当且仅当$\frac{y}{x}$=$\frac{2x}{y}$即x=$\frac{2+\sqrt{2}}{2}$且y=1+$\sqrt{2}$时取等号,
故选:C
点评 本题考查基本不等式求最值,属基础题.

练习册系列答案
相关题目
18.由函数y=lg(1-2x)的图象得到函数y=lg(3-2x)的图象,只需要( )
| A. | 向左平移1个单位 | B. | 向右平移1个单位 | C. | 向左平移2个单位 | D. | 向右平移2个单位 |
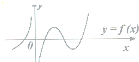 已知函数y=f(x)在定义域内可导,且图象如图所示,则此导函数y=f′(x)的图象可知为图中的( )
已知函数y=f(x)在定义域内可导,且图象如图所示,则此导函数y=f′(x)的图象可知为图中的( )