题目内容

12．一个四棱柱的三视图如图所示，则其表面积为16+8$\sqrt{2}$．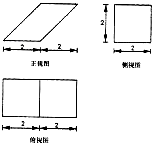

分析 根据几何体的三视图，得出该几何体是底面边长为2的正方形，且上底的一条棱在下底面的射影与下底的一条棱重合，
再根据图中的数据，求出该四棱柱的表面积．

解答 解：根据几何体的三视图，得，
该几何体是如图所示的四棱柱；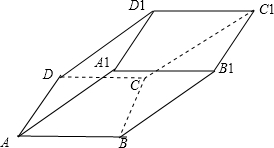
底面ABCD是边长为2的正方形，
且棱A1D1在底面ABCD内的射影是BC，
∴该四棱柱的表面积为
2S正方形ABCD+2${S}_{平行四边形A{{BB}_{1}A}_{1}}$+2${S}_{矩形A{{DD}_{1}A}_{1}}$
=2×22+2×2×2+2×2×$\sqrt{{2}^{2}{+2}^{2}}$
=16+8$\sqrt{2}$．
故答案为：16+8$\sqrt{2}$．

点评 本题以三视图为背景，通过由三视图想象实际几何体及其主要特征，重点考查空间想象能力与推理论证能力．

练习册系列答案
相关题目
13．已知命题p：实数t满足t2-5at+4a2＜0（其中a≠0），命题q：方程$\frac{{x}^{2}}{t-2}+\frac{{y}^{2}}{t-6}=1$表示双曲线
（1）若a=1，且p∧q为真命题，求实数t的取值范围；
（2）若p是q的必要不充分条件，求实数a的取值范围．
14．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）上的点到焦点距离的最大值为$\sqrt{2}$+1，离心率为$\frac{{\sqrt{2}}}{2}$．
（Ⅰ）求椭圆C的方程；
（Ⅱ）若过点M（2，0）的直线与椭圆C交于A，B两点，设P为椭圆上一点，且满足$\overrightarrow{OA}$+$\overrightarrow{OB}$=t$\overrightarrow{OP}$（O为坐标原点），当|$\overrightarrow{PA}$-$\overrightarrow{PB}$|＜$\frac{2\sqrt{5}}{3}$时，求实数t的取值范围．
11．把在标有1～8号数字的标牌中抽取一张后放回的事件称为一次随机实验，Pn是n次实验中抽取的8号标牌的次数为奇数的概率，求：Pn．
7．已知F1，F2是椭圆C：$\frac{{x}^{2}}{3}$+$\frac{{y}^{2}}{4}$=1的两个焦点，过F1的直线与椭圆C交于M，N两点，则△F2MN的周长为8．
17．已知直线y=kx+1与椭圆$\frac{{x}^{2}}{5}$+$\frac{{y}^{2}}{m}$=1恒有公共点，则实数m的取值范围为（　　）
A．m≥1B．m≥1或0＜m＜1C．m≥1且m≠5D．0＜m＜5且m≠1
4．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）经过点M（4，2），且离心率为$\frac{\sqrt{2}}{2}$，点R（x0，y0）是椭圆上的任意一点，从原点O引圆R：（x-x0）2+（y-y0）2=8的两条切线分别交椭圆C于点P，Q．
（Ⅰ）求椭圆C的方程；
（Ⅱ）求证：OP2+OQ2的值为定值．
1．已知F1、F2是椭圆$\frac{{x}^{2}}{49}$+$\frac{{y}^{2}}{24}$=1的两个焦点，A为椭圆上一点，则△AF1F2的周长为（　　）
A．4$\sqrt{6}$B．12C．14D．24
2．已知双曲线C：$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$，点P（2，1）在C的渐近线上，则C的率心率为$\frac{\sqrt{5}}{2}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网