题目内容
1.设二次函数f(x)=x2+bx+c(b,c∈R)的导函数为f′(x),关于x的方程f(x)=f′(x)有两个相等 实根,则$\frac{{b}^{2}}{1+{c}^{2}}$的最大值为( )| A. | 2$\sqrt{2}$-2 | B. | 2$\sqrt{2}$+2 | C. | $\frac{1}{2}$ | D. | 1 |
分析 由f(x)=f′(x)化为:x2+(b-2)x+c-b=0,由于关于x的方程f(x)=f′(x)有两个相等实数根,可得△=0,可得$c=\frac{{b}^{2}+4}{4}$,代入$\frac{{b}^{2}}{1+{c}^{2}}$,再利用基本不等式的性质即可得出.
解答 解:f′(x)=2x+b,f(x)=f′(x)化为:x2+(b-2)x+c-b=0,
∵关于x的方程f(x)=f′(x)有两个相等实数根,
∴△=(b-2)2-4(c-b)=0,
化为$c=\frac{{b}^{2}+4}{4}$,
∴$\frac{{b}^{2}}{1+{c}^{2}}$=$\frac{{b}^{2}}{1+\frac{({b}^{2}+4)^{2}}{16}}$=$\frac{16}{{b}^{2}+\frac{32}{{b}^{2}}+8}$≤$\frac{16}{2\sqrt{{b}^{2}•\frac{32}{{b}^{2}}}+8}$=2$\sqrt{2}$-2,当且仅当b2=4$\sqrt{2}$,c=$\sqrt{2}$+1时取等号.
∴$\frac{{b}^{2}}{1+{c}^{2}}$的最大值为$2\sqrt{2}$-2.
故选:A.
点评 本题考查了导数的运算法则、一元二次方程有实数根与判别式的关系、基本不等式的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
11.如图,在公路MN的两侧有四个村镇:A1、B1、C1、D1通过小路和公路相连,各路口分别是A、B、C、D,现要在公路上建一个长途汽车站,为使各村镇村民到汽车站所走的路程总和最小,汽车站应建在( )
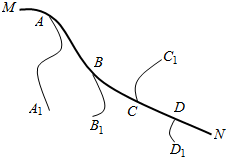

| A. | A处 | B. | D处 | ||
| C. | B、C间的任何一处(包括B、C) | D. | A、B之间的任何一处(包括A、B) |
12.已知F1,F2是椭圆上的两个焦点,过F1且与椭圆长轴垂直的直线交椭圆于A,B两点,若△ABF2是正三角形,则这个椭圆的离心率是( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{2}}{3}$ |
9.阅读程序图,该程序图输出的结果是( )


| A. | 94 | B. | 92 | C. | 95 | D. | 93 |
6.命题“若p,则q”的否命题为( )
| A. | 若¬p,则q | B. | 若p,则¬q | C. | 若¬p,则¬q | D. | 若q,则p |
10. 如图,在长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=1,则异面直线AC1与BB1所成的角的余弦值为( )
如图,在长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=1,则异面直线AC1与BB1所成的角的余弦值为( )
 如图,在长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=1,则异面直线AC1与BB1所成的角的余弦值为( )
如图,在长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=1,则异面直线AC1与BB1所成的角的余弦值为( )| A. | $\frac{2\sqrt{2}}{3}$ | B. | $\frac{\sqrt{2}}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{\sqrt{2}}{2}$ |