题目内容
9.定于在R上的函数f(x)满足f(x+2)=2f(x),当x∈(0,2]时,f(x)=$\left\{\begin{array}{l}{{x}^{2}-x,x∈(0,1]}\\{-lo{g}_{2}x,x∈(1,2]}\end{array}\right.$,若x∈(-2,0]时,f(x)≤k有解,则实数k的取值范围( )| A. | [-1,+∞) | B. | [-$\frac{1}{2},+∞$) | C. | [-$\frac{1}{2},-\frac{1}{8}$] | D. | [-$\frac{1}{8},+∞$) |
分析 根据已知中函数f(x)满足f(x+2)=2f(x),当x∈(0,2]时,f(x)=$\left\{\begin{array}{l}{{x}^{2}-x,x∈(0,1]}\\{-lo{g}_{2}x,x∈(1,2]}\end{array}\right.$,求出x∈(-2,0]时,函数的最小值,可得实数k的取值范围.
解答 解:当x∈(0,2]时,f(x)=$\left\{\begin{array}{l}{{x}^{2}-x,x∈(0,1]}\\{-lo{g}_{2}x,x∈(1,2]}\end{array}\right.$,
故当x∈(0,2]时,函数的值域为:[-1,0],
又由函数f(x)满足f(x+2)=2f(x),
∴x∈(-2,0]时,f(x)的值域为:[-$\frac{1}{2}$,0],
若x∈(-2,0]时,f(x)≤k有解,
则k≥$-\frac{1}{2}$,
即实数k的取值范围是[-$\frac{1}{2},+∞$),
故选:B.
点评 本题考查的知识点是分段函数,存在性问题,解答的关键是将存在性问题,转化为最值问题.

练习册系列答案
相关题目
20.某几何体的三视图如图所示,且该几何体的体积是2,则正视图中的x=( )
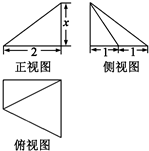

| A. | 2 | B. | 3 | C. | $\frac{4}{15}$ | D. | $\frac{4}{5}$ |
4.设全集U=R,集合A={x|0≤x≤2},B={x|x<1},则集合∁R(A∪B)=( )
| A. | (-∞,2] | B. | (2,+∞) | C. | (-∞,1] | D. | (-∞,0)∪[1,+∞) |
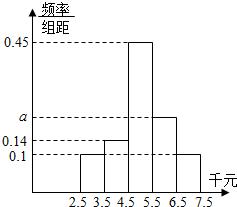 两会结束后,房价问题仍是国民关注的热点问题,某高校金融学一班的学生对某城市居民对房价的承受能力(如能买每平方米6千元的房子即承受能力为6千元)的调查作为社会实践,进行调查统计,将承受能力数据按区间[2.5,3.5),[3.5,4.5),[4.5,5.5),[5.5,6.5),[6.5,7.5](千元)进行分组,得到如下统计图:
两会结束后,房价问题仍是国民关注的热点问题,某高校金融学一班的学生对某城市居民对房价的承受能力(如能买每平方米6千元的房子即承受能力为6千元)的调查作为社会实践,进行调查统计,将承受能力数据按区间[2.5,3.5),[3.5,4.5),[4.5,5.5),[5.5,6.5),[6.5,7.5](千元)进行分组,得到如下统计图: