题目内容
19.已知f(x)=sin(2x+)(1)求f(-)的值.
(2)若θ为锐角,f(2θ)+f(-2θ)=,求tanθ的值.
分析 (1)由条件利用诱导公式求得f(-)的值.
(2)由条件利用两角和差的正弦公式求得 cos4θ 的值,可得cos2θ的值,再利用同角三角函数的基本关系求得tanθ的值.
解答 解:(1)f(-)=sin(-π+)=sin(-)=-sin=-.
(2)∵θ为锐角,f(2θ)+f(-2θ)=sin(4θ+)+sin(-4θ+)
=sin4θcos+cos4θsin-sin4θcos+cos4θsin=2cos4θsin=cos4θ=,
∴cos4θ=.
由于4θ∈(0,2π),故4θ∈(0,),或4θ∈(,2π).
若4θ∈(0,),cos4θ==2cos22θ-1,∴cos2θ===,
∴tan2θ==5-2,∴tanθ=-.
若4θ∈(,2π),cos4θ==2cos22θ-1,∴cos2θ=-==,
∴tan2θ==5+2,∴tanθ=+.
点评 本题主要考查同角三角函数的基本关系,诱导公式,两角和差的正弦公式,体现了分类讨论的数学思想,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.定于在R上的函数f(x)满足f(x+2)=2f(x),当x∈(0,2]时,f(x)=,若x∈(-2,0]时,f(x)≤k有解,则实数k的取值范围( )
| A. | [-1,+∞) | B. | [-) | C. | [-] | D. | [-) |
10.执行如图所示的程序框图,若输出的y=,则输入的x的值可能为( )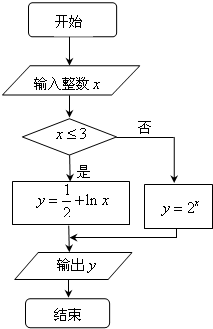

| A. | -1 | B. | 0 | C. | 1 | D. | 5 |
4.如图是一个算法的流程图,则输出S的值是( )
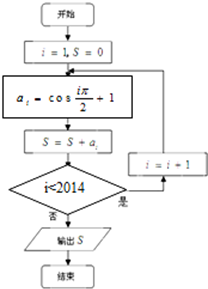

| A. | 2012 | B. | 2013 | C. | 2014 | D. | 2015 |
