题目内容
19.曲线y=x3-x2-x+1在点(0,1)处的切线方程是x+y-1=0.分析 求出函数的导数,求得切线的斜率,由直线的斜截式即可得到切线方程.
解答 解:y=x3-x2-x+1的导数为y′=3x2-2x-1,
曲线y=x3-x2-x+1在点(0,1)处的切线斜率为k=0-0-1=-1,
即有曲线y=x3-x2-x+1在点(0,1)处的切线方程为y=-x+1,
即为x+y-1=0.
故答案为:x+y-1=0.
点评 本题考查导数的运用:求切线方程,主要考查导数的几何意义,直线方程的求法,属于基础题.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
9.定于在R上的函数f(x)满足f(x+2)=2f(x),当x∈(0,2]时,f(x)=$\left\{\begin{array}{l}{{x}^{2}-x,x∈(0,1]}\\{-lo{g}_{2}x,x∈(1,2]}\end{array}\right.$,若x∈(-2,0]时,f(x)≤k有解,则实数k的取值范围( )
| A. | [-1,+∞) | B. | [-$\frac{1}{2},+∞$) | C. | [-$\frac{1}{2},-\frac{1}{8}$] | D. | [-$\frac{1}{8},+∞$) |
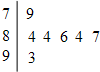 在校英语节演讲比赛中,七位评委老师为某班选手打出的分数的茎叶图(如图所示),去掉一个最高分和一个最低分后,所剩数据的方差为$\frac{8}{5}$.
在校英语节演讲比赛中,七位评委老师为某班选手打出的分数的茎叶图(如图所示),去掉一个最高分和一个最低分后,所剩数据的方差为$\frac{8}{5}$.