题目内容
1.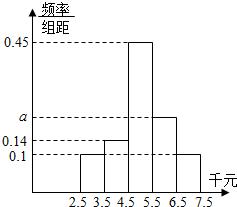 两会结束后,房价问题仍是国民关注的热点问题,某高校金融学一班的学生对某城市居民对房价的承受能力(如能买每平方米6千元的房子即承受能力为6千元)的调查作为社会实践,进行调查统计,将承受能力数据按区间[2.5,3.5),[3.5,4.5),[4.5,5.5),[5.5,6.5),[6.5,7.5](千元)进行分组,得到如下统计图:
两会结束后,房价问题仍是国民关注的热点问题,某高校金融学一班的学生对某城市居民对房价的承受能力(如能买每平方米6千元的房子即承受能力为6千元)的调查作为社会实践,进行调查统计,将承受能力数据按区间[2.5,3.5),[3.5,4.5),[4.5,5.5),[5.5,6.5),[6.5,7.5](千元)进行分组,得到如下统计图:(1)求a的值,并估计该城市居民的平均承受能力是多少元;
(2)若用分层抽样的方法,从承受能力在[3.5,4.5)与[5.5,6.5)的居民中抽取5人,在抽取的5人中随机取2人,求2人的承受能力不同的概率.
分析 (1)根据各组的累积频率为1,构造关于a的方程,解方程可得a的值,累加每组组中值与频率的积,可估算出该城市居民的平均承受能力是多少元;
(2)先计算出在抽取的5人中随机取2人的情况种数,再计算出2人的承受能力不同的情况种数,代入古典概型概率计算公式,可得答案.
解答 解:(1)由各组的累积频率为1,
可得:0.1+0.1+0.14+0.45+a=1,
所以a=0.21,(2分)
平均承受能力$\overline x=3×0.1+4×0.14+5×0.45+6×0.21+7×0.1=5.07$,
即城市居民的平均承受能力大约为5070元; (5分)
(2)用分层抽样的方法在这两组中抽5人,
即[3.5,4.5)组中抽2人与[5.5,6.5)抽3人,
设[3.5,4.5)组中两人为A1,A2,[5.5,6.5)组中三人为B1,B2,B2,
从这5人中随机取2人,有
A1A2,A1B1,A1B2,A1B3,A2B1,
A2B2,A2B3,B1B2,B1B3,B2B3共10中,
符合两人承受能力不同的有
A1B1,A1B2,A1B3,A2B1,A2B2,A2B3共6中,
所以所求概率为$P=\frac{6}{10}=\frac{3}{5}$.(12分)
点评 本题考查的知识点是古典概型概率计算公式,频率分布直方图,是统计和概率的综合应用,难度不大,属于基础题.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
12.函数y=cos(2x+$\frac{π}{6}$)的图象可由函数y=sin2x的图象( )
| A. | 向左平移$\frac{π}{3}$个单位而得到 | B. | 向右平移$\frac{π}{3}$个单位而得到 | ||
| C. | 向左平移$\frac{π}{6}$个单位而得到 | D. | 向右平移$\frac{π}{6}$个单位而得到 |
9.定于在R上的函数f(x)满足f(x+2)=2f(x),当x∈(0,2]时,f(x)=$\left\{\begin{array}{l}{{x}^{2}-x,x∈(0,1]}\\{-lo{g}_{2}x,x∈(1,2]}\end{array}\right.$,若x∈(-2,0]时,f(x)≤k有解,则实数k的取值范围( )
| A. | [-1,+∞) | B. | [-$\frac{1}{2},+∞$) | C. | [-$\frac{1}{2},-\frac{1}{8}$] | D. | [-$\frac{1}{8},+∞$) |
16.设i是虚数单位,若复数$z=\frac{{{a^2}+ai}}{1-i}>0$,则a的值为( )
| A. | 0或-1 | B. | 0或1 | C. | -1 | D. | 1 |
10.执行如图所示的程序框图,若输出的y=$\frac{1}{2}$,则输入的x的值可能为( )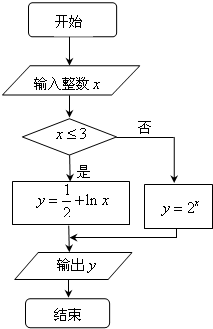

| A. | -1 | B. | 0 | C. | 1 | D. | 5 |