题目内容

18．已知?ABCD的两个顶点坐标分别为A（4，2），B（5，7），对角线交点为E（-3，4），求另外两个顶点C、D的坐标．

分析 利用平行四边形的性质得到向量相等，利用向量相等得到C，D坐标．

解答 解：因为?ABCD的两个顶点坐标分别为A（4，2），B（5，7），对角线交点为E（-3，4），
所以$\overrightarrow{AE}=\overrightarrow{EC}$，设C（x，y），则（-7，2）=（x+3，y-4），所以x+3=-7，y-4=2，解得x=-10，y=6，所以C（-10，6）；
$\overrightarrow{BE}=\overrightarrow{ED}$，设D（a，b），则（-8，-3）=（a+3，b-4），所以a+3=-8，b-4=-3，解得a=-11，b=1，所以D（-11，1）．

点评 本题考查了利用向量相等求点的坐标；坐标表示的向量相等，横坐标、纵坐标分别相等．

练习册系列答案
相关题目
8．在△ABC中，角A、B、C的对边分别是a、b、c，点（a，b）在直线x（sinA-sinB）+ysinB=csinC上．
（1）求C的大小；
（2）若c=7，求△ABC的周长的取值范围．
9．定于在R上的函数f（x）满足f（x+2）=2f（x），当x∈（0，2]时，f（x）=$\left\{\begin{array}{l}{{x}^{2}-x，x∈（0，1]}\\{-lo{g}_{2}x，x∈（1，2]}\end{array}\right.$，若x∈（-2，0]时，f（x）≤k有解，则实数k的取值范围（　　）
A．[-1，+∞）B．[-$\frac{1}{2}，+∞$）C．[-$\frac{1}{2}，-\frac{1}{8}$]D．[-$\frac{1}{8}，+∞$）
6．某种产品的加工需要5道工序，问如果其中某一工序不能放在最后，有多少种排列加工顺序的方法？
13．已知集合A={-1，1，3}，B={2，2a-1}，A∩B={1}，则实数a的值是1．
3．以双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的右顶点A为圆心作与渐近线相切的圆，过左焦点F作该圆的切线，设切点为P，切线与y轴的交点为M，且FM：MP=8：3，求双曲线的离心率．
10．执行如图所示的程序框图，若输出的y=$\frac{1}{2}$，则输入的x的值可能为（　　）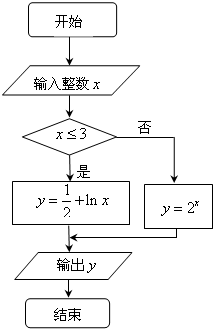
A．-1B．0C．1D．5
7．已知数列{an}满足a1=4，a2=2，an+2=$\frac{3+（-1）^{n}}{2}$an+2[1-（-1）n]，n∈N*，k∈N*．
（Ⅰ）求a3，a4，并直接写出an；
（Ⅱ）设Sk=a1+a3+…+a2k-1，Tk=a2+a4+…+a2k，分别求Sk，Tk关于k的表达式；
（Ⅲ）设Wk=$\frac{{2{S_k}}}{{2+{T_k}}}$，求使Wk＞2的所有k的值，并说明理由．
8．已知直线x+y-a=0与圆x2+y2=2交于A、B两点，O是坐标原点，向量$\overrightarrow{OA}$、$\overrightarrow{OB}$满足条件|$\overrightarrow{OA}$+$\overrightarrow{OB}$|=|$\overrightarrow{OA}$-$\overrightarrow{OB}$|，则实数a的值为（　　）
A．$\sqrt{2}$B．-$\sqrt{2}$C．±$\sqrt{2}$D．±1

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网