题目内容
14.设方程组$\left\{\begin{array}{l}{{x}^{3}-xyz=-5}\\{{y}^{3}-xyz=2}\\{{z}^{3}-xyz=21}\end{array}\right.$的正实数解为(x,y,z),则x+y+z=6.分析 利用作差法,结合立方差公式进行化简进行求解即可.
解答 解:由x3-xyz=-5,y3-xyz=2,
两式相减,得到(y-x)(x2+xy+y2)=7,
所以得到y-x=1或者y-x=7(舍去)
所以y-x=1,则x2+xy+y2=7
结合这个两个得到y=2,x=1
代入x3-xyz=-5中得到z=3
所以x+y+z=6,
故答案为:6.
点评 本题主要考查三次方程的求解,利用作差法是解决本题的关键.

练习册系列答案
相关题目
9.定于在R上的函数f(x)满足f(x+2)=2f(x),当x∈(0,2]时,f(x)=$\left\{\begin{array}{l}{{x}^{2}-x,x∈(0,1]}\\{-lo{g}_{2}x,x∈(1,2]}\end{array}\right.$,若x∈(-2,0]时,f(x)≤k有解,则实数k的取值范围( )
| A. | [-1,+∞) | B. | [-$\frac{1}{2},+∞$) | C. | [-$\frac{1}{2},-\frac{1}{8}$] | D. | [-$\frac{1}{8},+∞$) |
4.如图是一个算法的流程图,则输出S的值是( )
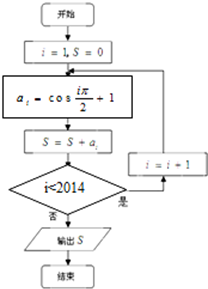

| A. | 2012 | B. | 2013 | C. | 2014 | D. | 2015 |