题目内容
3．设全集U={-2，-1，0，1，2}，集合A={1，2}，B={-2，1，2}，则A∪（∁UB）等于（ ）| A． | {-1，0，1，2} | B． | {1} | C． | {1，2} | D． | ∅ |
分析 根据全集U及B求出B的补集，找出A与B补集的并集即可．
解答 解：∵全集U={-2，-1，0，1，2}，集合A={1，2}，B={-2，1，2}，
∴∁UB={-1，0}，
则A∪（∁UB）={-1，0，1，2}，
故选：A．
点评 此题考查了交、并、补集的混合运算，熟练掌握各自的定义是解本题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
13．设F1，F2为椭圆的两焦点，B为椭圆短轴的一个端点，若△BF1F2为正三角形，则椭圆的离心率为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{\sqrt{2}}{2}$ | C． | $\frac{\sqrt{3}}{2}$ | D． | 2 |
14．一个几何体的三视图如图所示，则这个几何体的体积为（ ）
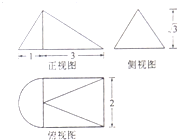
| A． | $\frac{（8+π）\sqrt{3}}{6}$ | B． | $\frac{（12+π）\sqrt{3}}{6}$ | C． | $\frac{（12+π）\sqrt{3}}{2}$ | D． | $\frac{（6+π）\sqrt{3}}{3}$ |
11．已知F1、F2是椭圆的两个焦点，以线段F1F2为边作正△MF1F2，若边MF1的中点在此椭圆上，则此椭圆的离心率为（ ）
| A． | $\frac{\sqrt{3}-1}{2}$ | B． | $\sqrt{2}$-1 | C． | $\frac{\sqrt{2}}{2}$ | D． | $\sqrt{3}$-1 |
18．圆x2+y2-2x+4y+3=0的圆心坐标为（ ）
| A． | （-2，4） | B． | （2，-4） | C． | （1，-2） | D． | （-1，2） |
8．对于集合M，定义函数fM（x）=$\left\{\begin{array}{l}{-1，x∈M}\\{1，x∉M}\end{array}\right.$，对于两个集合M、N，定义集合M⊕N={x|fM（x）•fN（x）=-1}，已知A={2，4，6，8，10}，B={1，2，4，5，6，8，9}，则集合A⊕B=（ ）
| A． | {1，5，9，10} | B． | {1，5，9} | C． | {2，4，6} | D． | {2，4，6，8} |