题目内容
15.已知函数f(x)=cos2x-sin2x+2sinxcosx.(1)求f(x)的单调递增区间;
(2)设α、β∈[0,$\frac{π}{2}$],f($\frac{α}{2}$+$\frac{π}{8}$)=$\frac{\sqrt{5}}{2}$,f($\frac{β}{2}$+π)=$\sqrt{2}$,求sin(α+β)的值.
分析 (1)由倍角公式化简函数解析式可得f(x)=$\sqrt{2}$sin(2x+$\frac{π}{4}$),由2kπ-$\frac{π}{2}$≤2x+$\frac{π}{4}$≤2kπ+$\frac{π}{2}$,k∈Z可解得f(x)的单调递增区间.
(2)由f($\frac{α}{2}$+$\frac{π}{8}$)=$\frac{\sqrt{5}}{2}$,可得:cosα,结合α范围可得sinα,由f($\frac{β}{2}$+π)=$\sqrt{2}$,可得sin($β+\frac{π}{4}$)=1,结合范围β∈[0,$\frac{π}{2}$],可解得β=$\frac{π}{4}$,从而由两角和的正弦函数公式即可计算求值.
解答 解:(1)∵f(x)=cos2x-sin2x+2sinxcosx
=cos2x+sin2x
=$\sqrt{2}$sin(2x+$\frac{π}{4}$)
∴由2kπ-$\frac{π}{2}$≤2x+$\frac{π}{4}$≤2kπ+$\frac{π}{2}$,k∈Z可解得f(x)的单调递增区间为:[kπ-$\frac{3π}{8}$,kπ+$\frac{π}{8}$],k∈Z.
(2)∵f($\frac{α}{2}$+$\frac{π}{8}$)=$\sqrt{2}$sin[2($\frac{α}{2}$+$\frac{π}{8}$)+$\frac{π}{4}$]=$\sqrt{2}$sin(α+$\frac{π}{2}$)=$\sqrt{2}$cosα=$\frac{\sqrt{5}}{2}$,
∴可得:cosα=$\frac{\sqrt{10}}{4}$,
∴由α∈[0,$\frac{π}{2}$],可得:sinα=$\sqrt{1-co{s}^{2}α}$=$\frac{\sqrt{6}}{4}$.
∵f($\frac{β}{2}$+π)=$\sqrt{2}$sin[2($\frac{β}{2}$+π)+$\frac{π}{4}$]=$\sqrt{2}$sin($β+\frac{π}{4}$)=$\sqrt{2}$,
∴可得sin($β+\frac{π}{4}$)=1,
∵β∈[0,$\frac{π}{2}$],可得:$β+\frac{π}{4}$∈[$\frac{π}{4}$,$\frac{3π}{4}$],
∴$β+\frac{π}{4}$=$\frac{π}{2}$,解得:β=$\frac{π}{4}$,
∴sin(α+β)=sinαcosβ+cosαsinβ=$\frac{\sqrt{6}}{4}$×$\frac{\sqrt{2}}{2}$+$\frac{\sqrt{10}}{4}$×$\frac{\sqrt{2}}{2}$=$\frac{\sqrt{3}+\sqrt{5}}{4}$.
点评 本题主要考查了两角和的正弦函数公式,倍角公式,同角三角函数关系式,诱导公式的应用,考查了正弦函数的图象和性质,属于基本知识的考查.

| A. | {-1,0,1,2} | B. | {1} | C. | {1,2} | D. | ∅ |
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |
| 信息技术 | 美术素描 | 音乐欣赏 | |
| 周一 | $\frac{1}{4}$ | $\frac{1}{4}$ | $\frac{1}{2}$ |
| 周三 | $\frac{1}{2}$ | $\frac{1}{2}$ | $\frac{2}{3}$ |
| 周五 | $\frac{1}{3}$ | $\frac{1}{3}$ | $\frac{2}{3}$ |
(2)设周三各辅导讲座满座的科目数为X,求随机变量X的分布列和数学期望.
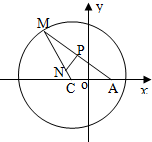 如图所示,已知圆C:(x+1)2+y2=8,定点A(1,0),M为圆上一动点,点P在线段AM上,点N在CM上,且满足$\overrightarrow{AM}$=2$\overrightarrow{AP}$,$\overrightarrow{NP}$•$\overrightarrow{AM}$=0,点N的轨迹为曲线E.求曲线E的方程.
如图所示,已知圆C:(x+1)2+y2=8,定点A(1,0),M为圆上一动点,点P在线段AM上,点N在CM上,且满足$\overrightarrow{AM}$=2$\overrightarrow{AP}$,$\overrightarrow{NP}$•$\overrightarrow{AM}$=0,点N的轨迹为曲线E.求曲线E的方程.