题目内容
14.一个几何体的三视图如图所示,则这个几何体的体积为( )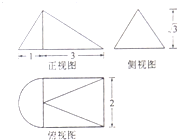
| A. | $\frac{(8+π)\sqrt{3}}{6}$ | B. | $\frac{(12+π)\sqrt{3}}{6}$ | C. | $\frac{(12+π)\sqrt{3}}{2}$ | D. | $\frac{(6+π)\sqrt{3}}{3}$ |
分析 根据几何体的三视图,得出该几何体是半圆锥体与四棱锥的组合体,根据图中数据即可求出它的体积.
解答 解:根据几何体的三视图,得;
该几何体是底面半径为1,高为$\sqrt{3}$的半圆锥体,
与底面为边长是2的正方形,高为$\sqrt{3}$的四棱锥的组合体;
该几何体的体积为
V几何体=V半圆锥体+V四棱锥
=$\frac{1}{2}$×$\frac{1}{3}$×π×12×$\sqrt{3}$+$\frac{1}{3}$×22×$\sqrt{3}$
=$\frac{(π+12)\sqrt{3}}{6}$.
故选:B.
点评 本题考查了空间几何体三视图的应用问题,也考查了空间想象能力与逻辑思维能力,是基础题目.

练习册系列答案
相关题目
2.已知函数f(x)=loga(x+1)(a>0,a≠1)在[0,1]上的值域是[0,1],若函数g(x)=ax-m-4的图象不过第二象限,则m的取值范围是( )
| A. | [-2,+∞) | B. | [-$\frac{1}{2}$,+∞) | C. | [-1,+∞) | D. | (-∞,2] |
9.设集合A={x|x2-x-2≤0},B={x|x≥a+1},若A?B,则a的取值范围是( )
| A. | a<2 | B. | a≥-2 | C. | a≤-2 | D. | a>2 |
3.设全集U={-2,-1,0,1,2},集合A={1,2},B={-2,1,2},则A∪(∁UB)等于( )
| A. | {-1,0,1,2} | B. | {1} | C. | {1,2} | D. | ∅ |
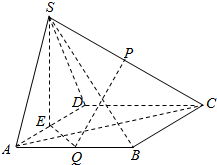 如图,在四棱锥S-ABCD中,底面ABCD为菱形,∠BAD=60°,平面SAD⊥平面ABCD,SA=SD,E,P,Q分别是棱AD,SC,AB的中点.
如图,在四棱锥S-ABCD中,底面ABCD为菱形,∠BAD=60°,平面SAD⊥平面ABCD,SA=SD,E,P,Q分别是棱AD,SC,AB的中点.