题目内容
11．已知F1、F2是椭圆的两个焦点，以线段F1F2为边作正△MF1F2，若边MF1的中点在此椭圆上，则此椭圆的离心率为（ ）| A． | $\frac{\sqrt{3}-1}{2}$ | B． | $\sqrt{2}$-1 | C． | $\frac{\sqrt{2}}{2}$ | D． | $\sqrt{3}$-1 |
分析 通过题意画出图形，利用勾股定理及椭圆的定义计算即得结论．
解答 
解：不妨设椭圆方程为：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0），
则M点必在y轴上，如图，连结PF2，
∵△MF1F2为正三角形，
∴PF1=$\frac{1}{2}$MF1=$\frac{1}{2}$F1F2=c，
PF2=$\sqrt{{F}_{1}{{F}_{2}}^{2}-P{{F}_{1}}^{2}}$=$\sqrt{3}$c=2a-c，
∴2a=（$\sqrt{3}$+1）c，即e=$\frac{c}{a}$=$\frac{\sqrt{3}+1}{2}$=$\sqrt{3}$-1，
故选：D．
点评 本题考查椭圆的简单性质，注意解题方法的积累，属于基础题．
练习册系列答案
考前必练系列答案
相关题目
1．椭圆$\frac{x^2}{4}+\frac{y^2}{m}=1$的焦距为2，则m的值为（ ）
| A． | 3 | B． | $\sqrt{15}$ | C． | 3或5 | D． | 3或$\sqrt{15}$ |
2．已知函数f（x）=loga（x+1）（a＞0，a≠1）在[0，1]上的值域是[0，1]，若函数g（x）=ax-m-4的图象不过第二象限，则m的取值范围是（ ）
| A． | [-2，+∞） | B． | [-$\frac{1}{2}$，+∞） | C． | [-1，+∞） | D． | （-∞，2] |
16．椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{2}$=1的短轴长为（ ）
| A． | $\sqrt{2}$ | B． | 2 | C． | 2$\sqrt{2}$ | D． | 4 |
3．设全集U={-2，-1，0，1，2}，集合A={1，2}，B={-2，1，2}，则A∪（∁UB）等于（ ）
| A． | {-1，0，1，2} | B． | {1} | C． | {1，2} | D． | ∅ |
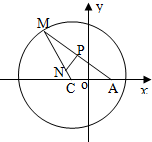如图所示，已知圆C：（x+1）2+y2=8，定点A（1，0），M为圆上一动点，点P在线段AM上，点N在CM上，且满足$\overrightarrow{AM}$=2$\overrightarrow{AP}$，$\overrightarrow{NP}$•$\overrightarrow{AM}$=0，点N的轨迹为曲线E．求曲线E的方程．