题目内容
13.设F1,F2为椭圆的两焦点,B为椭圆短轴的一个端点,若△BF1F2为正三角形,则椭圆的离心率为( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | 2 |
分析 利用△BF1F2为正三角形,确定几何量之间的关系,进而可求椭圆的离心率.
解答 解:由题意,设椭圆的半焦距长为c,则
∵△BF1F2为正三角形,
∴b=$\sqrt{3}$c
∴a2-c2=3c2
∴a=2c
∴e=$\frac{c}{a}$=$\frac{1}{2}$
故选:A.
点评 本题考查椭圆的几何性质,考查学生的计算能力,属于基础题.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
1.椭圆$\frac{x^2}{4}+\frac{y^2}{m}=1$的焦距为2,则m的值为( )
| A. | 3 | B. | $\sqrt{15}$ | C. | 3或5 | D. | 3或$\sqrt{15}$ |
8.若直线l:mx+ny=4和圆O:x2+y2=4没有交点,则过点(m,n)的直线与椭圆$\frac{x^2}{9}+\frac{y^2}{4}=1$的交点个数为( )
| A. | 0个 | B. | 至多有一个 | C. | 1个 | D. | 2个 |
18.椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的左焦点为F,斜率为$\sqrt{3}$的直线过F与椭圆交于M、N两点,且$\overrightarrow{MF}=2\overrightarrow{FN}$,则椭圆的离心率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{2}}}{3}$ | D. | $\frac{2}{3}$ |
2.已知函数f(x)=loga(x+1)(a>0,a≠1)在[0,1]上的值域是[0,1],若函数g(x)=ax-m-4的图象不过第二象限,则m的取值范围是( )
| A. | [-2,+∞) | B. | [-$\frac{1}{2}$,+∞) | C. | [-1,+∞) | D. | (-∞,2] |
3.设全集U={-2,-1,0,1,2},集合A={1,2},B={-2,1,2},则A∪(∁UB)等于( )
| A. | {-1,0,1,2} | B. | {1} | C. | {1,2} | D. | ∅ |
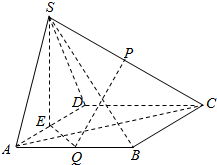 如图,在四棱锥S-ABCD中,底面ABCD为菱形,∠BAD=60°,平面SAD⊥平面ABCD,SA=SD,E,P,Q分别是棱AD,SC,AB的中点.
如图,在四棱锥S-ABCD中,底面ABCD为菱形,∠BAD=60°,平面SAD⊥平面ABCD,SA=SD,E,P,Q分别是棱AD,SC,AB的中点.