题目内容
12．f（x）是以5为周期的奇函数，f（-3）=4，且cos$α=\frac{1}{3}$，则f（9cos2α）=-4．分析 由二倍角公式可得cos2α=2cos2α-1=-$\frac{7}{9}$；再由函数的奇偶性与周期性求函数值．
解答 解：∵cos$α=\frac{1}{3}$，
∴cos2α=2cos2α-1=-$\frac{7}{9}$；
∴f（9cos2α）=f（-7），
又∵f（x）是以5为周期的奇函数，f（-3）=4；
∴f（-7）=f（3）=-f（-3）=-4；
故答案为：-4．
点评 本题考查了三角恒等式的应用及函数的性质应用，属于基础题．
练习册系列答案
相关题目
2．已知函数f（x）=loga（x+1）（a＞0，a≠1）在[0，1]上的值域是[0，1]，若函数g（x）=ax-m-4的图象不过第二象限，则m的取值范围是（ ）
| A． | [-2，+∞） | B． | [-$\frac{1}{2}$，+∞） | C． | [-1，+∞） | D． | （-∞，2] |
3．设全集U={-2，-1，0，1，2}，集合A={1，2}，B={-2，1，2}，则A∪（∁UB）等于（ ）
| A． | {-1，0，1，2} | B． | {1} | C． | {1，2} | D． | ∅ |
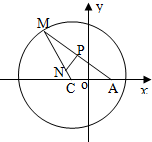如图所示，已知圆C：（x+1）2+y2=8，定点A（1，0），M为圆上一动点，点P在线段AM上，点N在CM上，且满足$\overrightarrow{AM}$=2$\overrightarrow{AP}$，$\overrightarrow{NP}$•$\overrightarrow{AM}$=0，点N的轨迹为曲线E．求曲线E的方程．
7．设a∈[0，4]，则使方程x2+ax+1=0有解的概率为（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{2}$ | D． | $\frac{3}{4}$ |
