题目内容
若函数f(x)＝
x3－
x2＋ax＋4恰在[－1,4]上单调递减，则实数a的值为________．
x3－x2＋ax＋4恰在[－1,4]上单调递减，则实数a的值为________．－4
∵f(x)＝x3－x2＋ax＋4，
∴f′(x)＝x2－3x＋a.又函数f(x)恰在[－1,4]上单调递减，
∴－1,4是f′(x)＝0的两根，∴a＝－1×4＝－4.
x3－x2＋ax＋4，∴f′(x)＝x2－3x＋a.又函数f(x)恰在[－1,4]上单调递减，
∴－1,4是f′(x)＝0的两根，∴a＝－1×4＝－4.
练习册系列答案
53随堂测系列答案
相关题目
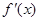是
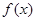的导函数，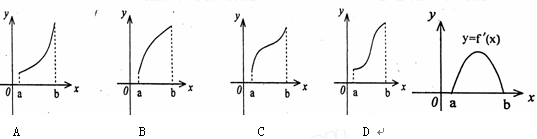
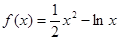的单调递减区间为（ ）
1,1）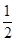
x2＋blnx在区间[
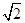，＋∞)上是减函数，则b的取值范围是________．
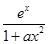，其中a为正实数．
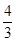时，求f(x)的极值点；②若f(x)为R上的单调函数，求a的取值范围．
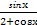的单调递增区间是 .
x2－ln x的单调递减区间为 ( )．