题目内容
函数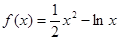 的单调递减区间为( )
的单调递减区间为( )
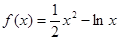 的单调递减区间为( )
的单调递减区间为( )A.( 1,1) 1,1) | B.(0,1] | C.[1,+∞) | D.( ∞,-1)∪(0,1] ∞,-1)∪(0,1] |
B
试题分析:因为
 ,所以由
,所以由 得
得 .又因为
.又因为 ,所以
,所以 .所求函数的单调递减区间为(0,1].
.所求函数的单调递减区间为(0,1].
练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
题目内容
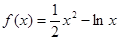 的单调递减区间为( )
的单调递减区间为( )A.( 1,1) 1,1) | B.(0,1] | C.[1,+∞) | D.( ∞,-1)∪(0,1] ∞,-1)∪(0,1] |
 ,所以由
,所以由 得
得 .又因为
.又因为 ,所以
,所以 .所求函数的单调递减区间为(0,1].
.所求函数的单调递减区间为(0,1].
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案