题目内容
已知a∈R，函数f(x)＝4x3－2ax＋a.
(1)求f(x)的单调区间；
(2)证明：当0≤x≤1时，f(x)＋|2－a|＞0.
(1)求f(x)的单调区间；
(2)证明：当0≤x≤1时，f(x)＋|2－a|＞0.
(1) 函数f(x)的单调递增区间为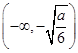
和
，
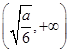单调递减区间为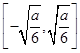
.
(2)见解析
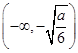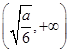和，单调递减区间为
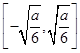.(2)见解析
(1)由题意得f′(x)＝12x2－2a.
当a≤0时，f′(x)≥0恒成立，此时f(x)的单调递增区间为(－∞，＋∞)．
当a＞0时，f′(x)＝12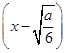
，
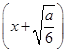此时函数f(x)的单调递增区间为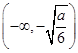和，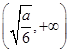
单调递减区间为.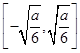
(2)证明：由于0≤x≤1，故当a≤2时，f(x)＋|a－2|＝4x3－2ax＋2≥4x3－4x＋2.
当a＞2时，f(x)＋|a－2|＝4x3＋2a(1－x)－2≥4x3＋4(1－x)－2＝4x3－4x＋2.
设g(x)＝2x3－2x＋1,0≤x≤1，则
g′(x)＝6x2－2＝6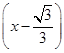
.
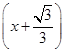于是
所以g(x)min＝g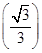
＝1－
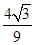＞0.
所以当0≤x≤1时，2x3－2x＋1＞0.
故f(x)＋|a－2|≥4x3－4x＋2＞0.
当a≤0时，f′(x)≥0恒成立，此时f(x)的单调递增区间为(－∞，＋∞)．
当a＞0时，f′(x)＝12
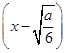
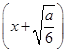，此时函数f(x)的单调递增区间为
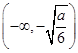和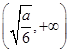，单调递减区间为
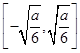.(2)证明：由于0≤x≤1，故当a≤2时，f(x)＋|a－2|＝4x3－2ax＋2≥4x3－4x＋2.
当a＞2时，f(x)＋|a－2|＝4x3＋2a(1－x)－2≥4x3＋4(1－x)－2＝4x3－4x＋2.
设g(x)＝2x3－2x＋1,0≤x≤1，则
g′(x)＝6x2－2＝6
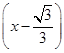
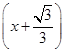.于是
| x | 0 | 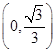 | 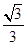 | 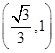 | 1 |
| g′(x) | | － | 0 | ＋ | |
| g(x) | 1 | 减 | 极小值 | 增 | 1 |
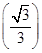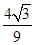＝1－＞0.所以当0≤x≤1时，2x3－2x＋1＞0.
故f(x)＋|a－2|≥4x3－4x＋2＞0.
练习册系列答案
字词句篇与同步作文达标系列答案
相关题目
R)，使得f(x)≥kx十b且g(x)≤kx＋b对一切x>0恒成立？若存在，求出该一次函数的表达式；若不存在，请说明理由．
，函数
,若
在
上是单调减函数，则
的取值范围是
x3－
x2＋ax＋4恰在[－1,4]上单调递减，则实数a的值为________．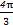
),f(-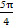
)的大小关系为 (用“<”连接).
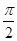时，
f′(x)＞0.则函数y＝f(x)－sin x在[－2π，2π]上的零点个数为________．