题目内容
【题目】已知圆
经过点
,
，圆心在直线
上
（1）求圆的标准方程；
（2）若直线
与圆C相切且与
轴截距相等，求直线的方程.
【答案】（1）
；（2）
【解析】
（1）由已知线段AB为圆C的弦，圆心C定在弦AB的垂直平分线上，写出线段AB垂直平分线方程，与直线
联立，即得圆心C坐标，计算|AC|长，即为圆C半径，从而可得圆的标准方程；（2）分两种情况考虑：当与坐标轴的截距为0时，设切线方程为y＝kx；当与坐标轴的截距不为0时，设切线方程为x+y＝b，利用圆心到直线的距离等于半径，可得切线方程．
（1）由题意可知AB为圆C的弦，其垂直平分线过圆心C，
∵A（0，0）和B（7，7），∴kAB＝1，线段AB垂直平分线的斜率为-1，
又线段AB的中点坐标为（
，），
∴线段AB的垂直平分线的方程为：y﹣＝-（x-），即x+y-7＝0，
又圆心在直线4x-3y＝0上，联立得：
，
解得：
，即圆心C坐标为（3，4），
∴圆C的半径|AC|＝5，
则圆C的方程为：（x-3）2+（y﹣4）2＝25；
（2）若直线过原点，设切线方程为y＝kx，即kx﹣y＝0，
圆心C到切线的距离d＝
，
整理得：16k2+24k+9＝0，解得：k＝
，
所求切线的方程为：y＝
；
若截距不为0时，设圆的切线方程为：x+y＝b，
圆心C到切线的距离d＝
＝r＝5，解得b＝7±5
，
所求切线方程为
，
综上，所有满足题意的切线方程有3条，分别为
.
阅读快车系列答案
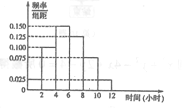
【题目】我校高二年级共2000名学生，其中男生1200人.为调查学生们的手机使用情况，采用分层抽样的方法，随机抽取100位学生每周平均使用手机上网时间的样本数据（单位：小时）.根据这100个数据，得到学生每周平均使用手机上网时间的频率分布直方图（如图所示），其中样本数据分组区间分别为
.
（1）应收集男生、女生样本数据各多少人？
（2）估计我校高二年级学生每周平均使用手机上网时间超过4小时的概率.
（3）将平均每周使用手机上网时间在
内定义为“长时间使用手机”，在
内定义为“短时间使用手机”.在样本数据中，有25名学生不近视.请完成下列2×2列联表，并判断是否有99.5%的把握认为“学生每周使用手机上网时间与近视程度有关”.
近视 | 不近视 | 合计 | |
长时间使用手机上网 | |||
短时间使用手机上网 | 15 | ||
合计 | 25 |
附：
| 0.100 | 0.050 | 0.010 | 0.005 |
| 2.706 | 6.635 | 7.879 |
