Question

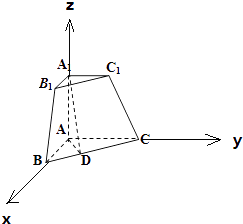
【题目】三棱锥被平行于底面ABC的平面所截得的几何体如图所示，截面为A1B1C1 ， ∠BAC=90°，A1A⊥平面ABC，A1A= ，AB= ，AC=2，A1C1=1， = ． （Ⅰ）证明：BC⊥平面A1AD
（Ⅱ）求二面角A﹣CC1﹣B的余弦值．

Answer 1

【答案】证明：（Ⅰ）以AB、AC、AA1分别为x轴、y轴、z轴建立空间直角坐标系， 则A（0，0，0），B（ ，0，0），C（0，2，0），A1（0，0， ）， ，
∵BD：DC=1：2， = ．
∴D（ ， ，0）， =（ ， ，0）， =（﹣ ）， =（0，0， ）．
∵ =0， =0，∴BC⊥AA1 ， BC⊥AD，又A1A∩AD=A，
BC⊥平面A1AD
解：（Ⅱ）∵BA平面ACC1A1 ， 取m= =（ ，0，0）为平面ACC1A1的法向量，
设平面BCC1B1的法向量为 =（l，m，n），则 =0， =0．
∴ ，l= ，n= ，取m=1，得 =（ ，1， ），
∴cos＜ ＞= = ．
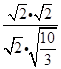∴二面角A﹣CC1﹣B的余弦值为 ．

【解析】（Ⅰ）以AB、AC、AA1分别为x轴、y轴、z轴建立空间直角坐标系，利用向量法能证明BC⊥平面A1AD．（Ⅱ）BA⊥平面ACC1A1 ， 取 = =（ ，0，0）为平面ACC1A1的法向量，
【考点精析】本题主要考查了直线与平面垂直的判定的相关知识点，需要掌握一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直；注意点：a)定理中的“两条相交直线”这一条件不可忽视；b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想才能正确解答此题．