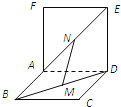
题目内容
【题目】己知⊙O:x2+y2=6,P为⊙O上动点,过P作PM⊥x轴于M,N为PM上一点,且 ![]() . (Ⅰ)求点N的轨迹C的方程;
. (Ⅰ)求点N的轨迹C的方程;
(Ⅱ)若A(2,1),B(3,0),过B的直线与曲线C相交于D、E两点,则kAD+kAE是否为定值?若是,求出该值;若不是,说明理由.
【答案】解:(Ⅰ)设N(x,y),P(x0 , y0),则M(x0 , 0), ![]() ,
, ![]()
由 ![]() ,得
,得  ,
,
∴ 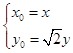
由于点P在圆O:x2+y2=6上,则有 ![]() ,即
,即 ![]() .
.
∴点N的轨迹C的方程为 ![]() .
.
(Ⅱ) 设D(x1 , y1),E(x2 , y2),过点B的直线DE的方程为y=k(x﹣3),
由 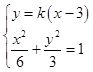 消去y得:(2k2+1)x2﹣12k2x+18k2﹣6=0,其中△>0
消去y得:(2k2+1)x2﹣12k2x+18k2﹣6=0,其中△>0
∴ ![]() ;
;
∴ ![]()
= 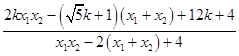
= 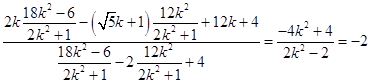
∴kAD+kAE是定值﹣2.
【解析】(Ⅰ)设M(x,y),则可设P(x,y0),Q(x,0),根据又 ![]() ,可确定y0=3y,进而可知点P的坐标代入圆的方程,求得曲线C的方程.(Ⅱ)设D(x1 , y1),E(x2 , y2),设出过点B的直线DE的方程,与题意方程联立,利用韦达定理求出横坐标的和与乘积,求出kAD+kAE化简即可判断否为定值.
,可确定y0=3y,进而可知点P的坐标代入圆的方程,求得曲线C的方程.(Ⅱ)设D(x1 , y1),E(x2 , y2),设出过点B的直线DE的方程,与题意方程联立,利用韦达定理求出横坐标的和与乘积,求出kAD+kAE化简即可判断否为定值.

【题目】一台机器按不同的转速生产出来的某机械零件有一些会有缺点,每小时生产有缺点零件的多少,随机器的运转的速度而变化,具有线性相关关系,下表为抽样试验的结果:
转速 | 8 | 10 | 12 | 14 | 16 |
每小时生产有缺点的零件数 | 5 | 7 | 8 | 9 | 11 |
(1)如果![]() 对
对![]() 有线性相关关系,求回归方程;
有线性相关关系,求回归方程;
(2)若实际生产中,允许每小时生产的产品中有缺点的零件最多有1个,那么机器的运转速度应控制在什么范围内?参考公式:![]() ,
,
 .
.
【题目】某校为了分析本校高中生的性别与是否喜欢数学之间的关系,在高中生中随机地抽取了90名学生调查,得到了如下列联表:
喜欢数学 | 不喜欢数学 | 总计 | |
男 | 30 | ① | 45 |
女 | ② | 25 | 45 |
总计 | ③ | ④ | 90 |
(1)求①②③④处分别对应的值;
(2)能有多大把握认为“高中生的性别与喜欢数学”有关?
附:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]() .
.