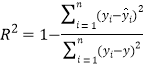题目内容
【题目】母线长为![]() ,底面半径为
,底面半径为![]() 的圆锥内有一球
的圆锥内有一球![]() ,与圆锥的侧面、底面都相切,现放入一些小球,小球与圆锥底面、侧面、球
,与圆锥的侧面、底面都相切,现放入一些小球,小球与圆锥底面、侧面、球![]() 都相切,这样的小球最多可放入__________个.
都相切,这样的小球最多可放入__________个.
【答案】10
【解析】由题意可知圆锥轴截面为正三角形,高为3,如图所示:
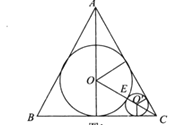
设球O半径为R,由∠OCB=30°,可得OC=2R,故OA=OC=2R,所以R+2R=3
∴R=1,OC=2,故得EC=1.设小球半径为r,同理可得![]() ,故
,故![]() ,所以小球半径为
,所以小球半径为![]() ,且
,且![]() .这时
.这时![]() 到直线AO的距离为
到直线AO的距离为![]() 。这些小球相邻相切,排在一起,则球心在一个半径为
。这些小球相邻相切,排在一起,则球心在一个半径为![]() 的圆M上,如图所示:
的圆M上,如图所示:
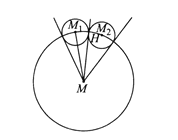
H为相邻两球切点, ![]() 分别为相邻两球球心,设∠
分别为相邻两球球心,设∠![]() ,则
,则![]() ,
,![]() ,由三角函数的性质可知
,由三角函数的性质可知![]() ,
,
∴![]() ,∴
,∴![]() ,,
,, ![]() ,∵
,∵![]()
![]() ,故可得能放入小球个数最多为10
,故可得能放入小球个数最多为10
故答案为:10

【题目】“共享单车”的出现,为我们提供了一种新型的交通方式。某机构为了调查人们对此种交通方式的满意度,从交通拥堵不严重的A城市和交通拥堵严重的B城市分别随机调查了20个用户,得到了一个用户满意度评分的样本,并绘制出茎叶图如图:

(1)根据茎叶图,比较两城市满意度评分的平均值的大小及方差的大小(不要求计算出具体值,给出结论即可);
(2)若得分不低于80分,则认为该用户对此种交通方式“认可”,否则认为该用户对此种交通方式“不认可”,请根据此样本完成此2×2列联表,并据此样本分析是否有95%的把握认为城市拥堵与认可共享单车有关;
A | B | 合计 | |
认可 | |||
不认可 | |||
合计 |
(3)在A,B城市对此种交通方式“认可”的用户中按照分层抽样的方法抽取6人,若在此6人中推荐2人参加“单车维护”志愿活动,求A城市中至少有1人的概率。
参考数据如下:(下面临界值表供参考)
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式 ,其中
,其中![]() )
)
【题目】已知某种植物每日平均增长高度![]() (单位:
(单位:![]() )与每日光照时间
)与每日光照时间![]() (单位:
(单位:![]() )之间的关系有如下一组数据:
)之间的关系有如下一组数据:
| 6 | 7 | 8 | 9 | 10 |
| 3.5 | 5.2 | 7 | 8.6 | 10.7 |
(1)求![]() 关于
关于![]() 的回归直线方程;
的回归直线方程;
(2)计算相关指数![]() 的值,并说明回归模型拟合程度的好坏;
的值,并说明回归模型拟合程度的好坏;
(3)若某天光照时间为8.5小时, 预测该天这种植物的平均增长高度(结果精确到0.1)
参考公式及数据: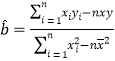 ,
,![]() ,
,![]() ,
,![]()
![]() ,
,,