题目内容
【题目】已知
， 
， 
， 
.给出以下三个命题：
①分别过点
， 
，作
的不同于
轴的切线，两切线相交于点
，则点
的轨迹为椭圆的一部分；
②若
， 
相切于点
，则点
的轨迹恒在定圆上；
③若
， 
相离，且
，则与
， 
都外切的圆的圆心在定椭圆上.
则以上命题正确的是（ ）
A. ①② B. ①③ C. ②③ D. ①②③
【答案】A
【解析】对于①，如图所示，
，
故点M恒在以E，F为焦点，AB为长轴的椭圆上，①正确；
对于②，若
与x轴相切于点A， 
与x轴相切于点B，由题意知
相外切，且
， 
相切于点H，过点Ｈ作两圆公切线，交ｘ轴于点Ｑ，如图所示，
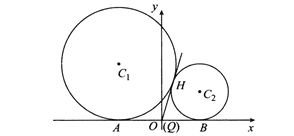
则
，故Ｑ与Ｏ点重合，所以
，故点Ｈ的轨迹恒在定圆上，②正确；
对于③设与
， 
都相切的圆的圆心为Ｔ，半径为ｒ，则Ｔ满足
， 
，得到
，故圆心T的轨迹是双曲线的一部分，③不正确，
故选：A
培优好卷单元加期末卷系列答案
一线名师权威作业本系列答案
【题目】某工厂的
,
,
三个不同车间生产同一产品的数量(单位:件)如下表所示.质检人员用分层抽样的方法从这些产品中共抽取6件样品进行检测:
车间 |
|
|
|
数量 | 50 | 150 | 100 |
(1)求这6件样品中来自,,各车间产品的数量;
(2)若在这6件样品中随机抽取2件进行进一步检测,求这2件产品来自相同车间的概率.
【题目】北京联合张家口获得2022年第24届冬奥会举办权，我国各地掀起了发展冰雪运动的热潮，现对某高中的学生对于冰雪运动是否感兴趣进行调查，该高中男生人数是女生的1.2倍，按照分层抽样的方法，从中抽取110人，调查高中生“是否对冰雪运动感兴趣”得到如下列联表：
感兴趣 | 不感兴趣 | 合计 | |
男生 | 40 | ||
女生 | 30 | ||
合计 | 110 |
（1）补充完成上述
列联表；
（2）是否有99%的把握认为是否喜爱冰雪运动与性别有关.
附：
（其中
）.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
