题目内容
【题目】在平面直角坐标系中,定义![]() 为两点
为两点![]() 、
、
![]() 的“切比雪夫距离”,又设点
的“切比雪夫距离”,又设点![]() 及
及![]() 上任意一点
上任意一点![]() ,称
,称![]() 的最小值为点
的最小值为点![]() 到
到
直线![]() 的“切比雪夫距离”,记作
的“切比雪夫距离”,记作![]() ,给出下列三个命题:
,给出下列三个命题:
① 对任意三点![]() 、
、![]() 、
、![]() ,都有
,都有![]() ;
;
② 已知点![]() 和直线
和直线![]() ,则
,则![]() ;
;
③ 定点![]() 、
、![]() ,动点
,动点![]() 满足
满足![]() (
(![]() ),
),
则点![]() 的轨迹与直线
的轨迹与直线![]() (
(![]() 为常数)有且仅有2个公共点;
为常数)有且仅有2个公共点;
其中真命题的个数是( )
A. 0 B. 1 C. 2 D. 3
【答案】D
【解析】设![]() ,由题意可得:
,由题意可得:
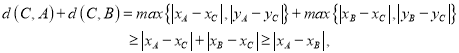
同理可得: ![]() ,则:
,则:
![]() ,
,
命题①成立;
设点Q是直线y=2x-1上一点,且Q(x,2x-1),可得![]() ,
,
由![]() ,解得
,解得![]() ,即有
,即有![]() ,当
,当![]() 时取得最小值
时取得最小值![]() ;
;
由![]() ,解得
,解得![]() 或
或![]() ,即有
,即有![]() ,
,
![]() 的范围是
的范围是![]() ,无最小值.
,无最小值.
综上可得,P,Q两点的“切比雪夫距离”的最小值为![]() .
.
说法②正确.
定点![]() 、
、![]() ,动点
,动点![]() 满足
满足![]() (
(![]() ),则:
),则:
![]() ,
,
显然上述方程所表示的曲线关于原点对称,故不妨设x≥0,y≥0.
(1)当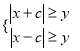 时,有
时,有![]() ,得:
,得: ![]() ;
;
(2)当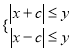 时,有
时,有![]() ,此时无解;
,此时无解;
(3)当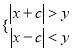 时,有
时,有![]() ;
;
则点P的轨迹是如图所示的以原点为中心的两支折线.
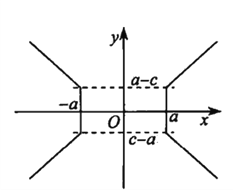
结合图象可知,点![]() 的轨迹与直线
的轨迹与直线![]() (
(![]() 为常数)有且仅有2个公共点,命题③正确.
为常数)有且仅有2个公共点,命题③正确.
综上可得命题①②③均正确,真命题的个数是3.
本题选择D选项.

练习册系列答案
相关题目

