题目内容
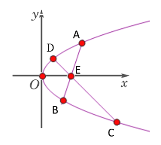
【题目】已知双曲线![]() 的左、右顶点分别为
的左、右顶点分别为![]() ,直线
,直线![]() 与双曲线交于
与双曲线交于![]() ,直线
,直线![]() 交直线
交直线![]() 于点
于点![]() .
.
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)若点![]() 的轨迹与矩形
的轨迹与矩形![]() 的四条边都相切,探究矩形
的四条边都相切,探究矩形![]() 对角线长是否为定值,若是,求出此值;若不是,说明理由.
对角线长是否为定值,若是,求出此值;若不是,说明理由.

【答案】(1) ![]() ;(2)见解析.
;(2)见解析.
【解析】试题分析:(1)利用交轨法,求出点![]() 的轨迹方程;(2) 设点
的轨迹方程;(2) 设点![]() ,过点
,过点![]() 作椭圆的切线,则切线的斜率存在且不为0,设斜率为
作椭圆的切线,则切线的斜率存在且不为0,设斜率为![]() ,则切线方程为
,则切线方程为![]() ,
,
代入到椭圆方程整理,得![]() .由
.由![]() 得到
得到
![]() ,这个关于
,这个关于![]() 的一元二次方程的两根即为
的一元二次方程的两根即为![]() 与
与![]() ,
,
由![]() ,可知
,可知![]() ,即
,即![]() ,即点
,即点![]() 为矩形
为矩形![]() 外接圆的圆心,其中
外接圆的圆心,其中![]() 为直径,大小为
为直径,大小为![]() ,故矩形
,故矩形![]() 对角线长为定值
对角线长为定值![]() .
.
试题解析:
(1)设点![]() ,
, ![]() ,
, ![]() ,其中
,其中![]() .
.
由题意,得![]() ,
, ![]() .
.
由![]() ,①
,①
![]() ,②
,②
两式相乘得![]() .
.
∵![]() ,
,
∴![]() ,
,
代入上式得
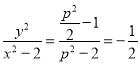
![]() ,
,
由①与![]() ,得
,得![]() ,
,
①÷②,得![]() .
.
故点![]() 的轨迹方程为
的轨迹方程为![]() .
.
(2)设点![]() ,过点
,过点![]() 作椭圆的切线,
作椭圆的切线,
则切线的斜率存在且不为0,设斜率为![]() ,
,
则切线方程为![]() ,
,
代入到椭圆方程整理,
得![]() .
.
![]()
![]() ,
,
即![]() .
.
这个关于![]() 的一元二次方程的两根即为
的一元二次方程的两根即为![]() 与
与![]() ,
,
由![]() ,
,
得![]() .
.
设![]() 为坐标原点,故可知
为坐标原点,故可知![]() ,
,
同理,得![]() ,
,
即点![]() 为矩形
为矩形![]() 外接圆的圆心,其中
外接圆的圆心,其中![]() 为直径,大小为
为直径,大小为![]() ,
,
故矩形![]() 对角线长为定值
对角线长为定值![]() .
.

 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案【题目】2015年12月10日,我国科学家屠呦呦教授由于在发现青蒿素和治疗疟疾的疗法上的贡献获得诺贝尔医学奖,以青蒿素类药物为主的联合疗法已经成为世界卫生组织推荐的抗疟疾标准疗法,目前,国内青蒿人工种植发展迅速,调查表明,人工种植的青蒿的长势与海拨高度、土壤酸碱度、空气湿度的指标有极强的相关性,现将这三项的指标分别记为![]() ,并对它们进行量化:0表示不合格,1表示临界合格,2表示合格,再用综合指标
,并对它们进行量化:0表示不合格,1表示临界合格,2表示合格,再用综合指标![]() 的值评定人工种植的青蒿的长势等级,若
的值评定人工种植的青蒿的长势等级,若![]() ,则长势为一级;若
,则长势为一级;若![]() ,则长势为二极;若
,则长势为二极;若![]() ,则长势为三级,为了了解目前人工种植的青蒿的长势情况,研究人员随机抽取了10块青蒿人工种植地,得到如下结果:
,则长势为三级,为了了解目前人工种植的青蒿的长势情况,研究人员随机抽取了10块青蒿人工种植地,得到如下结果:
种植地编号 |
|
|
|
|
|
|
|
|
|
|
|
种植地编号 |
|
|
|
|
|
|
|
|
|
|
|
(1)若该地有青蒿人工种植地180个,试估计该地中长势等级为三级的个数;
(2)从长势等级为一级的青蒿人工种植地中随机抽取两个,求这两个人工种植地的综合指标![]() 均为4个概率.
均为4个概率.