Question

【题目】已知圆C过点,且与圆外切于点,过点作圆C的两条切线PM,PN,切点为M,N.

(1)求圆C的标准方程;

(2)试问直线MN是否恒过定点?若过定点,请求出定点坐标.

Answer 1

【答案】(1).(2)直线MN过定点.

【解析】

（1）由题意可知圆C的圆心在y轴上,设半径为r,则圆心,再由圆C过点，代入解得，即可得到圆的方程.

（2）由题意可得,则M,N,P,C四点共圆,且该圆以PC为直径,圆心坐标为,即可得到圆的方程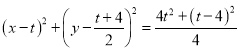，再求出两圆的公共弦的方程即可得解.

解:(1)由题意可知圆C的圆心在y轴上,设半径为r,则圆心,

故圆C的标准方程为.

因为圆C过点,所以,解得,

故圆C的标准方程为.

(2)由题意可得,则M,N,P,C四点共圆,且该圆以PC为直径,圆心坐标为,

故该圆的方程是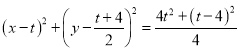,即.

因为圆C的方程为,所以公共弦MN所在直线方程为,

整理得.

令解得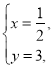

故直线MN过定点.