题目内容
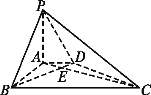
【题目】如图,在三棱柱ABC﹣A1B1C1中,D,E分别是B1C1、BC的中点,∠BAC=90°,AB=AC=2,A1A=4,A1E= ![]() .
.
(Ⅰ)证明:A1D⊥平面A1BC;
(Ⅱ)求二面角A﹣BD﹣B1的平面角的正弦值.
【答案】(Ⅰ)证明:∵在三棱柱ABC﹣A1B1C1中,D,E分别是B1C1、BC的中点,∠BAC=90°,AB=AC=2, ∴A1D∥AE,AE⊥BC,AE=BE= ![]() ,
,
∵A1A=4,A1E= ![]() .
.
∴A1E2+AE2= ![]() ,∴AE⊥A1E,
,∴AE⊥A1E,
∵A1E∩BC=E,∴AE⊥平面A1BC,
∵A1D∥AE,∴A1D⊥平面A1BC.
(Ⅱ)解:如图,以BC中点O为坐标原点,以OB、OA、OA1所在直线分别为x、y、z轴建系.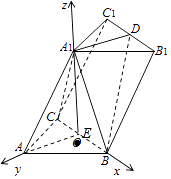
易知A1(0,0, ![]() ),B(
),B( ![]() ,0,0),C(﹣
,0,0),C(﹣ ![]() ,0,0),
,0,0),
A(0, ![]() ,0),D(0,﹣
,0),D(0,﹣ ![]() ,
, ![]() ),B1(
),B1( ![]() ,﹣
,﹣ ![]() ,
, ![]() ),
),
设平面A1BD的法向量为 ![]() =(x,y,z),
=(x,y,z),
由 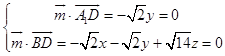 ,可取
,可取 ![]() .
.
设平面B1BD的法向量为 ![]() =(x,y,z),
=(x,y,z),
由 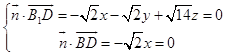 ,可取
,可取 ![]() .
.
cos< ![]() >=
>= ![]()
又∵该二面角为钝角,
∴二面角A1﹣BD﹣B1的平面角的余弦值为﹣ ![]() .
.
【解析】(1)先证AE⊥平面A1BC,再证A1D∥AE即可‘’(2)所求值即为平面A1BD的法向量与平面B1BD的法向量的夹角的余弦值的绝对值的相反数,计算即可.
【考点精析】解答此题的关键在于理解直线与平面垂直的判定的相关知识,掌握一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想.

【题目】为了增强环保意识,某社团从男生中随机抽取了60人,从女生中随机抽取了50人参加环保知识测试,统计数据如下表所示:
优秀 | 非优秀 | 总计 | |
男生 | 40 | 20 | 60 |
女生 | 20 | 30 | 50 |
总计 | 60 | 50 | 110 |
(1)试判断是否有99%的把握认为环保知识是否优秀与性别有关;
(2)为参加市举办的环保知识竞赛,学校举办预选赛,现在环保测试优秀的同学中选3人参加预选赛,已知在环保测试中优秀的同学通过预选赛的概率为![]() ,若随机变量
,若随机变量![]() 表示这3人中通过预选赛的人数,求
表示这3人中通过预选赛的人数,求![]() 的分布列与数学期望.
的分布列与数学期望.
附:![]() =
=![]()
| 0.500 | 0.400 | 0.100 | 0.010 | 0.001 |
| 0.455 | 0.708 | 2.706 | 6.635 | 10.828 |