Question

【题目】如图,在底面为直角梯形的四棱锥P-ABCD中,AD∥BC,∠ABC=90°,PA⊥平面ABCD,PA=3,AD=2,AB=2,BC=6.

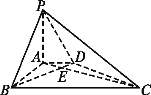
(1)求证:BD⊥平面PAC; (2)求二面角P-BD-A的大小.

Answer 1

【答案】(1)见解析;(2)60°.

【解析】分析：（1）由PA⊥平面ABCD，知BD⊥PA．由tan∠ABD==，tan∠BAC==，知∠ABD=30°，∠BAC=60°．由此能够证明BD⊥平面PAC．（2）连接PE，由BD⊥平面PAC，知BD⊥PE，BD⊥AE．所以∠AEP为二面角P﹣BD﹣A的平面角，由此能够求出二面角P﹣BD﹣A的大小．

详解：（1）∵PA⊥平面ABCD，BD平面ABCD．

∴BD⊥PA．

∵tan∠ABD==，tan∠BAC==，

∴∠ABD=30°，∠BAC=60°．

∴∠AEB=90°，即BD⊥AC．

∵PA∩AC=A，∴BD⊥平面PAC．

（2）连接PE，

∵BD⊥平面PAC，∴BD⊥PE，BD⊥AE．

∴∠AEP为二面角P﹣BD﹣A的平面角．

在Rt△AEB中，AE=ABsin∠ABD=，

∴tan∠AEP=，

∴∠AEP=60°，

∴二面角P﹣BD﹣A的大小为60°．