Question

【题目】如图,已知抛物线C:x2=4y,过点M(0,2)任作一直线与C相交于A,B两点,过点B作y轴的平行线与直线AO相交于点D(O为坐标原点).

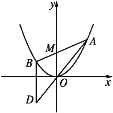
(1)证明动点D在定直线上;

(2)作C的任意一条切线l(不含x轴),与直线y=2相交于点N1,与(1)中的定直线相交于点N2,证明|MN2|2-|MN1|2为定值,并求此定值.

Answer 1

【答案】(1)证明见解析.

(2)证明见解析；|MN2|2-|MN1|2为定值8.

【解析】分析：（1）设，方程为，则为方程的解，从而，而，利用前者可以得到，从而在定直线上.

（2）设切线方程为，由直线和抛物线相切可以得到，从而得到的坐标，它们和有关，利用两点之间的距离公式可以得到.

详解：(1)证明:依题意可设方程为，代入，

得 ，即.

设，则有，

直线的方程为； 的方程为.

解得交点的坐标，注意到 及，

则有.

因此点在定直线.

(2)解:依题设,切线的斜率存在且不等于,设切线的方程为，

代入得，即.

由得，化简整理得.

故切线的方程可写为.

分别令得的坐标为，，

则，即为定值.