题目内容
【题目】已知函数![]() ,若在定义域内存在
,若在定义域内存在![]() ,使得
,使得![]() 成立,则称
成立,则称![]() 为函数
为函数![]() 的局部对称点.
的局部对称点.
(1)若![]() ,证明:函数
,证明:函数![]() 必有局部对称点;
必有局部对称点;
(2)若函数![]() 在区间
在区间![]() 内有局部对称点,求实数
内有局部对称点,求实数![]() 的取值范围;
的取值范围;
(3)若函数![]() 在
在![]() 上有局部对称点,求实数
上有局部对称点,求实数![]() 的取值范围.
的取值范围.
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]()
【解析】
试题分析:(1)利用题中所给的定义,通过二次函数的判别式大于0,证明二次函数有局部对称点;(2)利用方程有解,通过换元,转化为打钩函数有解问题,利用函数的图象,确定实数c的取值范围;(3)利用方程有解,通过换元,转化为二次函数在给定区间有解,建立不等式组,通过解不等式组,求得实数的取值范围.
试题解析:(1)由![]() 得
得![]() =
=![]() ,代入
,代入![]() 得,
得,
![]() =
=![]() ,得到关于
,得到关于![]() 的方程
的方程![]() =
=![]() ).
).
其中![]() ,由于
,由于![]() 且
且![]() ,所以
,所以![]() 恒成立,
恒成立,
所以函数![]() =
=![]() )必有局部对称点.
)必有局部对称点.
(2)方程![]() =
=![]() 在区间
在区间![]() 上有解,于是
上有解,于是![]() ,
,
设![]() ),
),![]() ,
,![]() ,
,
其中![]() ,所以
,所以![]() .
.
(3)![]() ,由于
,由于![]() ,
,
所以![]() =
=![]() .
.
于是![]() =
=![]() (*)在
(*)在![]() 上有解.
上有解.
令![]() ),则
),则![]() ,
,
所以方程(*)变为![]() =
=![]() 在区间
在区间![]() 内有解,
内有解,
需满足条件: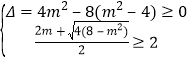 .
.
即![]() ,,化简得
,,化简得![]() .
.

 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案【题目】为了对2016年某校中考成绩进行分析,在60分以上的全体同学中随机抽出8位,他们的数学分数(已折算为百分制)从小到大排是60、65、70、75、80、85、90、95,物理分数从小到大排是72、77、80、84、88、90、93、95. 参考公式:相关系数 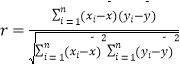 ,
,
回归直线方程是: ![]() ,其中
,其中  ,
,
参考数据: ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
(1)若规定85分以上为优秀,求这8位同学中恰有3位同学的数学和物理分数均为优秀的概率;
(2)若这8位同学的数学、物理、化学分数事实上对应如下表:
学生编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
数学分数x | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 |
物理分数y | 72 | 77 | 80 | 84 | 88 | 90 | 93 | 95 |
化学分数z | 67 | 72 | 76 | 80 | 84 | 87 | 90 | 92 |
①用变量y与x、z与x的相关系数说明物理与数学、化学与数学的相关程度;
②求y与x、z与x的线性回归方程(系数精确到0.01),当某同学的数学成绩为50分时,估计其物理、化学两科的得分.

