题目内容
已知数列{an}的前n项和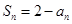 ,数列{bn}满足b1=1,b3+b7=18,且
,数列{bn}满足b1=1,b3+b7=18,且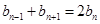 (n≥2).(1)求数列{an}和{bn}的通项公式;(2)若
(n≥2).(1)求数列{an}和{bn}的通项公式;(2)若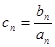 ,求数列{cn}的前n项和Tn.
,求数列{cn}的前n项和Tn.
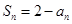 ,数列{bn}满足b1=1,b3+b7=18,且
,数列{bn}满足b1=1,b3+b7=18,且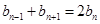 (n≥2).(1)求数列{an}和{bn}的通项公式;(2)若
(n≥2).(1)求数列{an}和{bn}的通项公式;(2)若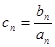 ,求数列{cn}的前n项和Tn.
,求数列{cn}的前n项和Tn.(1) ,(2)
,(2) .
.
 ,(2)
,(2) .
.试题分析:(1)由
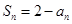 及
及 进行相减求得
进行相减求得 与
与 的关系,由等比数列定义可得数列{
的关系,由等比数列定义可得数列{ }的通项公式,又由
}的通项公式,又由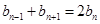 可知数列{bn}是等差数列,进而可求得其通项公式;(2)易得
可知数列{bn}是等差数列,进而可求得其通项公式;(2)易得 ,其通项为等差乘等比型,可用错位相乘法求其前n项和Tn.
,其通项为等差乘等比型,可用错位相乘法求其前n项和Tn.试题解析:(1)由题意知
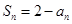 ①,当n≥2时,
①,当n≥2时, ②,①-②得
②,①-②得 ,即
,即 ,又
,又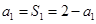 ,∴
,∴ ,故数列{an}是以1为首项,
,故数列{an}是以1为首项, 为公比的等比数列,所以
为公比的等比数列,所以 ,由
,由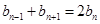 (n≥2)知,数列{bn}是等差数列,设其公差为d,则
(n≥2)知,数列{bn}是等差数列,设其公差为d,则 ,故
,故 ,综上,数列{an}和{bn}的通项公式分别为
,综上,数列{an}和{bn}的通项公式分别为 .
.(2)∵
 ,∴
,∴
 ③
③ ④
④③-④得
 ,
,即
 ,
,∴

 与
与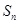 的关系:
的关系: ,等差与等比数列的定义和通项公式,数列求和方法:错位相减法.
,等差与等比数列的定义和通项公式,数列求和方法:错位相减法.
练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
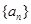 为等差数列,且
为等差数列,且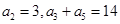 ,则
,则 ( )
( )  ,
, ,…,
,…, 中最大的项为( )
中最大的项为( )



 是首项为1,公差为2的等差数列,
是首项为1,公差为2的等差数列, 表示
表示 项和.
项和. 及
及 是首项为2的等比数列,公比
是首项为2的等比数列,公比 满足
满足 ,求
,求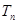 .
. 为等差数列,若
为等差数列,若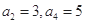 ,则
,则 的值为( ).
的值为( ).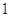



 是等差数列,首项
是等差数列,首项 ,则使前n项和
,则使前n项和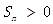 成立的最大自然数n是_______.
成立的最大自然数n是_______.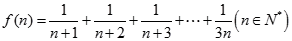 ,则
,则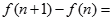 ( )
( )



 中,
中, ,则数列
,则数列 等于
等于